题目内容
(本题满分16分)
(文科学生做)已知命题p:函数![]() 在R上存在极值;
在R上存在极值;
命题q:设A={x| x 2 + 2 x 3<0}, B={x| x 2 (a +1) x + a >0},若对![]() ,都有
,都有![]() ;
;
若![]() 为真,
为真,![]() 为假,试求实数a的取值范围。
为假,试求实数a的取值范围。
(理科学生做)已知命题p:对![]() ,函数
,函数![]() 有意义;
有意义;
命题q:设A={x| x 2 + 2 x 3<0}, B={x| x 2 (a +1) x + a >0},若对![]() ,都有
,都有![]() ;
;
若![]() 为真,
为真,![]() 为假,试求实数a的取值范围。
为假,试求实数a的取值范围。
解析:(文科)由题意得:![]() , …………2分
, …………2分
因为f(x)在R上存在极值,所以![]() =0有两个不相等的实根;
=0有两个不相等的实根;
所以Δ=a2 4>0, 得a>2或a <2 …………5分
(理科)由题意得:对![]() 有ax2 4ax +a+6>0恒成立, …………2分
有ax2 4ax +a+6>0恒成立, …………2分
当a=0时,有6>0恒成立,
当a≠0时,则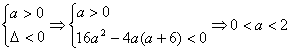
所以![]() …………5分
…………5分
命题q:由x2 + 2x 3<0得3<x <1 所以A=(3, 1) …………7分
因为对![]() ,都有
,都有![]() ,所以A
,所以A![]() B; …………8分
B; …………8分
由x 2 (a +1) x + a >0得(x a)(x 1)>0
当a<1时,B= ( ∞, a)∪(1, +∞), 此时不满足A![]() B,
B,
当a≥1时,B= ( ∞, 1)∪(a, +∞), 此时满足A![]() B,所以a≥1 …………10分
B,所以a≥1 …………10分
因为![]() 为真,
为真,![]() 为假,所以p与q一真一假, …………11分
为假,所以p与q一真一假, …………11分
(文科)当p真q假,则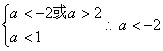 …………13分
…………13分
当p假 q真,则![]() …………15分
…………15分
所以所求a的取值范围是![]() 或
或![]() …………16分
…………16分
(理科)当p真q假,则![]() …………13分
…………13分
当p假 q真,则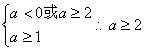 …………15分
…………15分
所以所求a的取值范围是![]() 或
或![]() …………16分
…………16分

 全能测控一本好卷系列答案
全能测控一本好卷系列答案

 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在