题目内容
11.在锐角△ABC中,角A,B,C的对边分别为a,b,c,若b=2,B=2A,则c的取值范围是($\sqrt{2}$,$\frac{4\sqrt{3}}{3}$).分析 由条件求得即$\frac{π}{6}$<A<$\frac{π}{4}$,再根据正弦定理求得c=$\frac{2sin3A}{sin2A}$=4cosA-$\frac{1}{cosA}$,显然c在($\frac{π}{6}$,$\frac{π}{4}$)上是减函数,由此求得c的范围.
解答 解:锐角△ABC中,∵B=2A<$\frac{π}{2}$,∴A<$\frac{π}{4}$.
再根据C=π-3A<$\frac{π}{2}$,可得A>$\frac{π}{6}$,即$\frac{π}{6}$<A<$\frac{π}{4}$,
再根据正弦定理可得$\frac{b}{sinB}$=$\frac{2}{sin2A}$=$\frac{c}{sinC}$=$\frac{c}{sin3A}$,
求得c=$\frac{2sin3A}{sin2A}$=$\frac{3-{4sin}^{2}A}{cosA}$=$\frac{{4cos}^{2}A-1}{cosA}$=4cosA-$\frac{1}{cosA}$ 在($\frac{π}{6}$,$\frac{π}{4}$)上是减函数,
故c∈($\sqrt{2}$,$\frac{4\sqrt{3}}{3}$),
故答案为:($\sqrt{2}$,$\frac{4\sqrt{3}}{3}$).
点评 本题主要考查三角形的内角和公式、正弦定理,函数的单调性的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.要得到函数g(x)=$sin(2x+\frac{π}{6})$,只需将f(x)=cos2x的图象( )
| A. | 左移$\frac{π}{3}$个单位 | B. | 右移$\frac{π}{3}$个单位 | C. | 左移$\frac{π}{6}$个单位 | D. | 右移$\frac{π}{6}$个单位 |
19.如图所示是某一几何体的三视图,则这个几何体是( )
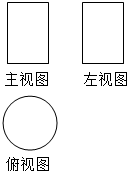

| A. | 圆柱体 | B. | 圆锥体 | C. | 正方体 | D. | 球体 |