题目内容
函数f(x)＝
在(－∞，＋∞)上单调，则a的取值范围是________．
(－∞，－
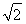]∪(1，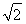
]
【解析】若a>0，则f(x)＝ax2＋1在[0，＋∞)上单调增，
∴f(x)＝(a2－1)eax在(－∞，0)上单调增，
∴
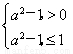∴1<a≤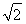
.同理，当a<0时，可求得a≤－
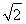，故a∈(－∞，－
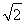]∪(1，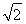
]
练习册系列答案
相关题目
题目内容
函数f(x)＝在(－∞，＋∞)上单调，则a的取值范围是________．
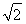(－∞，－]∪(1，]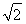
【解析】若a>0，则f(x)＝ax2＋1在[0，＋∞)上单调增，
∴f(x)＝(a2－1)eax在(－∞，0)上单调增，
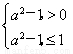∴∴1<a≤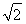.同理，当a<0时，可求得a≤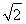－，故a∈(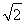－∞，－]∪(1，]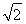
