题目内容
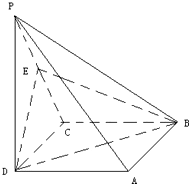 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.(1)证明:PA∥平面EDB;
(2)求EB与底面ABCD所成角的正切值;
(3)求二面角E-BD-C的余弦值.
分析:(1)欲证PA∥平面EDB,根据直线与平面平行的判定定理可知只需证PA与平面EDB内一直线平行,连接AC,交BD于O,连接EO,根据中位线定理可知EO∥PA,PA?平面EDB,EO?平面EDB,满足定理所需条件;
(2)作EM⊥DC于M,连接MB,根据线面所成角的定义可知∠EBM是EB与底面ABCD所成的角,而在△EBM中即可求出EB与底面ABCD所成角的正切值;
(3)作EH⊥BD于D,根据二面角平面角的定义可知∠EHM为二面角E-BD-C的平面角,在Rt△EMH中,求出此角的余弦值,即为二面角E-BD-C的余弦值.
(2)作EM⊥DC于M,连接MB,根据线面所成角的定义可知∠EBM是EB与底面ABCD所成的角,而在△EBM中即可求出EB与底面ABCD所成角的正切值;
(3)作EH⊥BD于D,根据二面角平面角的定义可知∠EHM为二面角E-BD-C的平面角,在Rt△EMH中,求出此角的余弦值,即为二面角E-BD-C的余弦值.
解答: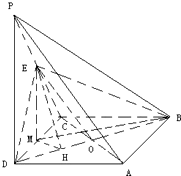 解:(1)证明:连接AC,交BD于O,连接EO.
解:(1)证明:连接AC,交BD于O,连接EO.
则O是AC的中点.∵E是PC的中点,∴EO∥PA
∵PA?平面EDB,EO?平面EDB,∴PA∥平面EDB
(2)在平面PDC中,作EM⊥DC于M,连接MB.
∵侧棱PD⊥底面ABCD,PD?平面PDC,
∴平面PDC⊥底面ABCD.∵EM⊥DC,平面PDC∩平面ABCD=DC
∴EM⊥平面ABCD∴∠EBM是EB与底面ABCD所成的角.
∵PD=2,且EM是△PDC的中位线,∴EM=1
而在直角△BCD中,∠BCD=90°,
∴BM=
∴tan∠EBM=
=
=
,
即EB与底面ABCD所成角的正切值为
.
(3)在平面EDB内,作EH⊥BD于H.
由(2)知,EM⊥平面ABCD,连接MH,则MH⊥BD.
∴∠EHM为二面角E-BD-C的平面角.
在Rt△DMH中,∠DHM=90°,∠CDB=45°,DM=1,
∴MH=
.∵EM=1,∴在Rt△EMH中,EH=
,
∴cos∠EHM=
=
,
即,二面角E-BD-C的余弦值为
.
 解:(1)证明:连接AC,交BD于O,连接EO.
解:(1)证明:连接AC,交BD于O,连接EO.则O是AC的中点.∵E是PC的中点,∴EO∥PA
∵PA?平面EDB,EO?平面EDB,∴PA∥平面EDB
(2)在平面PDC中,作EM⊥DC于M,连接MB.
∵侧棱PD⊥底面ABCD,PD?平面PDC,
∴平面PDC⊥底面ABCD.∵EM⊥DC,平面PDC∩平面ABCD=DC
∴EM⊥平面ABCD∴∠EBM是EB与底面ABCD所成的角.
∵PD=2,且EM是△PDC的中位线,∴EM=1
而在直角△BCD中,∠BCD=90°,
∴BM=
| 5 |
| EM |
| MB |
| 1 | ||
|
| ||
| 5 |
即EB与底面ABCD所成角的正切值为
| ||
| 5 |
(3)在平面EDB内,作EH⊥BD于H.
由(2)知,EM⊥平面ABCD,连接MH,则MH⊥BD.
∴∠EHM为二面角E-BD-C的平面角.
在Rt△DMH中,∠DHM=90°,∠CDB=45°,DM=1,
∴MH=
| ||
| 2 |
| ||
| 2 |
∴cos∠EHM=
| MH |
| EH |
| ||
| 3 |
即,二面角E-BD-C的余弦值为
| ||
| 3 |
点评:本题考查直线与平面平行的判定,以及直线与平面所成角和二面角及其度量,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.