题目内容
【题目】已知数列{an}为等比数列,其前n项和为Sn , 已知a1+a4=﹣ ![]() ,且对于任意的n∈N*有Sn , Sn+2 , Sn+1成等差数列;
,且对于任意的n∈N*有Sn , Sn+2 , Sn+1成等差数列;
(1)求数列{an}的通项公式;
(2)已知bn=n(n∈N+),记 ![]() ,若(n﹣1)2≤m(Tn﹣n﹣1)对于n≥2恒成立,求实数m的范围.
,若(n﹣1)2≤m(Tn﹣n﹣1)对于n≥2恒成立,求实数m的范围.
【答案】
(1)解:设等比数列{an}的公比为q,
∵对于任意的n∈N+有Sn,Sn+2,Sn+1成等差,
∴2 ![]() .
.
整理得: ![]() .
.
∵a1≠0,∴,2+2q+2q2=2+q.
∴2q2+q=0,又q≠0,∴q= ![]() .
.
又 ![]() ,
,
把q= ![]() 代入后可得
代入后可得 ![]() .
.
所以, ![]() ;
;
(2)解:∵bn=n, ![]() ,∴
,∴ ![]() ,
,
∴ ![]() .
.
![]() .
.
∴ ![]() =
= ![]()
∴ ![]() .
.
若(n﹣1)2≤m(Tn﹣n﹣1)对于n≥2恒成立,
则(n﹣1)2≤m[(n﹣1)2n+1+2﹣n﹣1]对于n≥2恒成立,
也就是(n﹣1)2≤m(n﹣1)(2n+1﹣1)对于n≥2恒成立,
∴m≥ ![]() 对于n≥2恒成立,
对于n≥2恒成立,
令 ![]() ,
,
∵ ![]() =
= ![]()
∴f(n)为减函数,∴f(n)≤f(2)= ![]() .
.
∴m ![]() .
.
所以,(n﹣1)2≤m(Tn﹣n﹣1)对于n≥2恒成立的实数m的范围是[ ![]() ).
).
【解析】(1)设出等比数列的公比,利用对于任意的n∈N+有Sn , Sn+2 , Sn+1成等差得2S3=S1+S2 , 代入首项和公比后即可求得公比,再由已知 ![]() ,代入公比后可求得首项,则数列{an}的通项公式可求;(2)把(1)中求得的an和已知b
,代入公比后可求得首项,则数列{an}的通项公式可求;(2)把(1)中求得的an和已知b![]() 整理,然后利用错位相减法求Tn , 把Tn代入(n﹣1)2≤m(Tn﹣n﹣1)后分离变量m,使问题转化为求函数的最大值问题,分析函数的单调性时可用作差法.
整理,然后利用错位相减法求Tn , 把Tn代入(n﹣1)2≤m(Tn﹣n﹣1)后分离变量m,使问题转化为求函数的最大值问题,分析函数的单调性时可用作差法.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系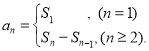 .
.


