题目内容
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
【答案】(Ⅰ)f(x)是奇函数(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】
(Ⅰ)先求定义域,再判断![]() 与f(x)关系,最后根据奇偶性定义作判断与证明,(Ⅱ)根据单调性定义进行判断,(Ⅲ)先根据单调性确定方程组,转化为一元二次方程有两正根,再根据二次方程实根分布列方程,最后解不等式组得结果.
与f(x)关系,最后根据奇偶性定义作判断与证明,(Ⅱ)根据单调性定义进行判断,(Ⅲ)先根据单调性确定方程组,转化为一元二次方程有两正根,再根据二次方程实根分布列方程,最后解不等式组得结果.
解:(Ⅰ)f(x)是奇函数;证明如下:
由![]() 解得x<-3或x>3,
解得x<-3或x>3,
所以f(x)的定义域为(-∞,-3)∪(3,+∞),关于原点对称.
∵![]() =
=![]() ,
,
故f(x)为奇函数/
(Ⅱ)任取x1,x2∈(3,+∞)且x1<x2,
![]() =
=![]() ,
,
∵(x1-3)(x2+3)-(x1+3)(x2-3)<0,∴(x1-3)(x2+3)<(x1+3)(x2-3),
即![]() ,
,
当m=![]() 时,
时,![]() ,即f(x1)<f(x2).
,即f(x1)<f(x2).
故f(x)在(3,+∞)上单调递减.
(Ⅲ)由(Ⅱ)知,当0<m<1时,f(x)在[α,β]上单调递减.
假设存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)].
则有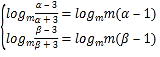 ,∴
,∴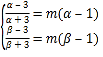 .
.
所以α,β是方程![]() 的两正根,
的两正根,
整理得mx2+(2m-1)x-3m+3=0在(0,+∞)有2个不等根α和β.
令h(x)=mx2+(2m-1)x-3m+3,则h(x)在(0,+∞)有2个零点,
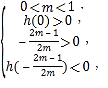 解得
解得![]() ,
,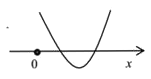
故m的取值范围为![]() .
.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()