题目内容
【题目】从![]() 中这
中这![]() 个数中取
个数中取![]() 个数组成递增等差数列,所有可能的递增等差数列这个数记为
个数组成递增等差数列,所有可能的递增等差数列这个数记为![]() .
.
(1)当![]() 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及![]() 的值;
的值;
(2)求![]() ;
;
(3)求证:![]() .
.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)通过列举,可知符合要求的递增等差数列为![]() 共
共![]() 个.所以
个.所以![]() ;(2)由于
;(2)由于![]() ,且
,且![]() ,即有
,即有![]() 项,所以
项,所以![]() ,故
,故![]() 取
取![]() ,
,![]() 取
取![]() 个,归纳出个数
个,归纳出个数![]() ;(3)由于
;(3)由于![]() ,按照(2)的方法,求出
,按照(2)的方法,求出![]() 的表达式,然后利用差比较法证明不等式.
的表达式,然后利用差比较法证明不等式.
试题解析:
(1) 符合要求的递增等差数列为![]() 共
共![]() 个.
个.![]() .
.
(2)设满足条件的一个等差数列首项为![]() ,公差为
,公差为![]() 的可能取值为
的可能取值为![]() .对于给定的
.对于给定的
![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个(如:
个(如: ![]() 时,
时,![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个:
个: ![]() ,其它同理)
,其它同理)![]() 当
当![]() 取
取![]() 时,可得符合要求的等差数列个数为:
时,可得符合要求的等差数列个数为:![]() .
.
(3)证明: 设等差数列首项为![]() ,公差为
,公差为![]() ,记
,记![]() 的整数部分是
的整数部分是![]() ,则
,则![]() ,即
,即![]() .
.![]() 的可能取值为
的可能取值为![]() ,对于给定的
,对于给定的![]() , 当
, 当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个.
个.![]() 当
当![]() 取
取![]() 时,符合要求的等差数列个数
时,符合要求的等差数列个数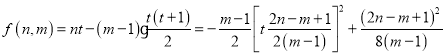 .由题意
.由题意![]() .又
.又 ,
,
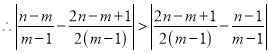 .
.
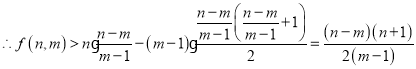 . 即
. 即![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目