题目内容
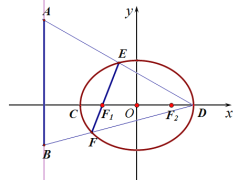
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.(i)
两点.(i)![]() ,求直线
,求直线![]() 的方程;(ii)直线
的方程;(ii)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)(i)直线
;(2)(i)直线![]() 的方程为
的方程为![]() ;(ii)存在常数
;(ii)存在常数![]() ,使得
,使得![]() 恒成立.
恒成立.
【解析】
(1)利用圆心到直线的距离等于半径构造关于![]() 的方程,解方程求得结果;(2)(i)设
的方程,解方程求得结果;(2)(i)设![]() ,由
,由![]() 可得
可得![]() ,代入圆的方程可求解出
,代入圆的方程可求解出![]() 点坐标,从而得到斜率,求得直线方程;(ii)将直线
点坐标,从而得到斜率,求得直线方程;(ii)将直线![]() 方程代入圆的方程可求得
方程代入圆的方程可求得![]() 点坐标;同理将直线
点坐标;同理将直线![]() 方程代入圆的方程可求得
方程代入圆的方程可求得![]() 点坐标;利用
点坐标;利用![]() 可求得
可求得![]() 的关系,利用
的关系,利用![]() 表示出
表示出![]() 点坐标,整理可得
点坐标,整理可得![]() ,进而可得到
,进而可得到![]() 满足
满足![]() ,得到常数
,得到常数![]() .
.
(1)由题意,![]()
![]() 圆心
圆心![]() 到直线
到直线![]() 的距离
的距离![]()
![]() 直线
直线![]() 与圆
与圆![]() 相切
相切 ![]() ,解得:
,解得:![]()
![]() 直线
直线![]() 方程为:
方程为:![]()
(2)(i)设![]() ,由
,由![]() 得:
得:![]()
由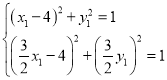 ,解得:
,解得: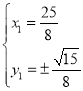
![]()
![]() 直线
直线![]() 的方程为:
的方程为:![]()
(ii)由题意知:![]() ,
,![]()
则![]() ,与圆
,与圆![]() 联立得:
联立得:![]()
![]()
![]()
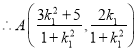
同理可得: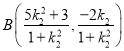
![]()
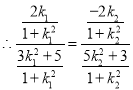 ,整理可得:
,整理可得:![]()
![]()
![]()
设![]()
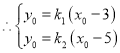

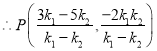 ,即
,即![]()
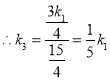
![]()
![]() 存在常数
存在常数![]() ,使得
,使得![]() 恒成立
恒成立

【题目】甲、乙两人参加一个射击的中奖游戏比赛,在相同条件下各打靶50次,统计每次打靶所得环数,得下列频数分布表.
环数 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的频数 | 0 | 1 | 4 | 7 | 14 | 16 | 6 | 2 |
乙的频数 | 1 | 2 | 5 | 6 | 10 | 16 | 8 | 2 |
比赛中规定所得环数为1,2,3,4时获奖一元,所得环数为5,6,7时获奖二元,所得环数为8,9时获奖三元,所得环数为10时获奖四元,没命中则无奖.
(1)根据上表,在答题卡给定的坐标系内画出甲射击50次获奖金额(单位:元)的条形图;

(2)估计甲射击1次所获奖至少为三元的概率;
(3)要从甲、乙两人中选拔一人参加射击比赛,请你根据甲、乙两人所获奖金额的平均数和方差作出选择.
【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: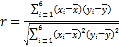 ,
,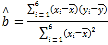
【题目】菜市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图1所示的频率分布南方匿,接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价
)进行了一次调查统计,制成了如图1所示的频率分布南方匿,接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1﹣13分别对应2018年1月至2019年1月).
(单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1﹣13分别对应2018年1月至2019年1月).
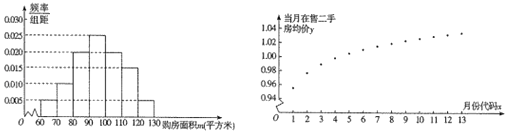
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房耐积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如表所示:
,并得到一些统计量的值,如表所示:
|
| |
|
|
|
|
| |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .参考公式:相关指数
.参考公式:相关指数 .
.