��Ŀ����
����Ŀ��ij�����ž��õķ�չ������������������������Ǹõ�һ����������������Ĵ��������������1
���x | 2011 | 2012 | 2013 | 2014 | 2015 |
������y��ǧ��Ԫ�� | 5 | 6 | 7 | 8 | 10 |
Ϊ���о�����ķ��㣬������Ա���ϱ������ݽ����˴�����![]() �õ���2��
�õ���2��
ʱ�����t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
��1����z����t�����Իع鷽�̣�
��2��ͨ����1���еķ��̣����y����x�Ļع鷽�̣�
��3��������ع鷽��Ԥ�2010����ף��õش������ɴ���٣�
�����������Իع鷽��![]() ��
��
����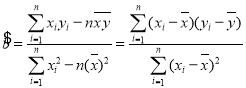 ,
, ![]() .
.
���𰸡���1��![]() ����2��
����2��![]() ����3��3.6ǧ�ڣ�
����3��3.6ǧ�ڣ�
��������
��1��������С���˷����z����t�����Իع鷽�̣�
��2��ͨ��![]() ����z����t�����Իع鷽�̻���y����x�Ļع鷽�̣�
����z����t�����Իع鷽�̻���y����x�Ļع鷽�̣�
��3�����ûع鷽�̴�����ֵ��
�⣺��1���ɱ������ݣ�����![]() ��1+2+3+4+5����3��
��1+2+3+4+5����3��
![]() ��0+1+2+3+5����2.2��
��0+1+2+3+5����2.2��
![]() tizi��1��0+2��1+3��2+4��3+5��5��45��
tizi��1��0+2��1+3��2+4��3+5��5��45��
![]() 12+22+32+42+52��55��
12+22+32+42+52��55��
����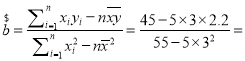 1.2��
1.2��
![]() b
b![]() 2.2��1.2��3����1.4��
2.2��1.2��3����1.4��
����z����t�����Իع鷽��Ϊz��1.2t��1.4��
��2����t��x��2010��z��y��5����z��1.2t��1.4�У��õ���
y��5��1.2��x��2010����1.4��
��y����x�Ļع鷽����y��1.2x��2408.4��
��3���ɣ�2��֪������x��2010ʱ��y��1.2��2010��2408.4��3.6��
��Ԥ�2010����ף��õش������ɴ�3.6ǧ�ڣ�

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�����Ŀ����������������չ��ƽ̨��ÿ�γɹ������������Ʒ�Ϳ���Ƿ����������ϵͳ.�Ӹ�����ϵͳ��ѡ��200�γɹ����ף����������۽���ͳ�ƣ������߶���Ʒ��������Ϊ0.70���Կ�ݵ�������Ϊ0.60,��Ʒ�Ϳ�ݶ�����Ľ���Ϊ80
����������֪������������![]() �����������ش��ܷ���99%��Ϊ�������߶���Ʒ������Կ������֮���й�ϵ����
�����������ش��ܷ���99%��Ϊ�������߶���Ʒ������Կ������֮���й�ϵ����
�Կ������ | �Կ�ݲ����� | �ϼ� | |
����Ʒ���� | 80 | ||
����Ʒ������ | |||
�ϼ� | 200 |
��������Ƶ����Ϊ���ʣ�ij���ڸ�����ƽ̨�Ͻ��е�3�ι����У������Ʒ�Ϳ�ݶ�����Ĵ���Ϊ�������![]() ����
����![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() .
.
����![]() ��
��
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |

