题目内容
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
【答案】(1) ![]() .
.
(2) 不存在这样的直线![]() .
.
【解析】试题分析:(I)用待定系数法即可求得圆C的标准方程;(Ⅱ)首先考虑斜率不存在的情况.当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2).l与圆C相交于不同的两点,那么Δ>0.由题设及韦达定理可得k与x1、x2之间关系式,进而求出k的值.若k的值满足Δ>0,则存在;若k的值不满足Δ>0,则不存在.
试题解析:(I)设圆C:(x-a)2+y2=R2(a>0),由题意知
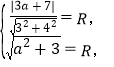 解得a=1或a=
解得a=1或a=![]() , 3分
, 3分
又∵S=πR2<13,
∴a=1,
∴圆C的标准方程为:(x-1)2+y2=4. 6分
(Ⅱ)当斜率不存在时,直线l为:x=0不满足题意.
当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2),
又∵l与圆C相交于不同的两点,
联立![]() 消去y得:(1+k2)x2+(6k-2)x+6=0, 9分
消去y得:(1+k2)x2+(6k-2)x+6=0, 9分
∴Δ=(6k-2)2-24(1+k2)=36k2-6k-5>0,
解得![]() 或
或![]() .
.
x1+x2=![]() ,y1+ y2=k(x1+x2)+6=
,y1+ y2=k(x1+x2)+6=![]() ,
,
![]() ,
,![]() ,
,
假设![]() ∥
∥![]() ,则
,则![]() ,
,
∴![]() ,
,
解得![]() ,假设不成立.
,假设不成立.
∴不存在这样的直线l. 13分

【题目】东莞市公交公司为了方便广大市民出行,科学规划公交车辆的投放,计划在某个人员密集流动地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 | 18 |
等候人数( | 16 | 19 | 23 | 26 | 29 | 33 |
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程,再用剩下的2组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“理想回归方程”:
(3)为了使等候的乘客不超过38人,试用(1)中方程估计间隔时间最多可以设置为多少分钟?
【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到表2:
得到表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程![]() ,
,
其中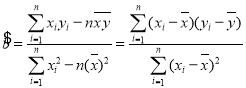 ,
, ![]() .
.
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: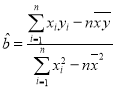 ,
,![]() ,
,![]() ,
,![]() .
.