题目内容

【题目】已知A（﹣1，1，2）、B（1，0，﹣1），设D在直线AB上，且 =2 ，设C（λ， +λ，1+λ），若CD⊥AB，则λ的值为（ ）
A.
B.﹣
C.
D.

【答案】B
【解析】解：设D（x，y，z），则

=（x+1，y﹣1，z﹣2），

=（2，﹣1，﹣3），

=（1﹣x，﹣y，﹣1﹣z），

∵ =2 ，

∴（x+1，y﹣1，z﹣2）=2（1﹣x，﹣y，﹣1﹣z）；

即 ，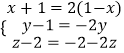

解得x= ，y= ，z=0；

∴D（ ， ，0），

=（ ﹣λ，﹣λ，﹣1﹣λ），

∵ ⊥ ，

∴ =2（ ﹣λ）+λ﹣3（﹣1﹣λ）=0，

解得λ=﹣ ．

所以答案是：B．

【考点精析】本题主要考查了共线向量与共面向量的相关知识点，需要掌握向量共线的充要条件：对于空间任意两个向量，，的充要条件是存在实数，使才能正确解答此题．

练习册系列答案
相关题目

【题目】椭圆C： 的左右焦点分别是F1 ， F2 ， 离心率为 ，过F1且垂直于x轴的直线被椭圆C截得的线段长为1．
（1）求椭圆C的方程；
（2）点P是椭圆C上除长轴端点外的任一点，连接PF1 ， PF2 ， 设∠F1PF2的角平分线PM交C的长轴于点M（m，0），求m的取值范围；
（3）在（2）的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点，设直线PF1 ， PF2的斜率分别为k1 ， k2 ， 若k≠0，试证明 为定值，并求出这个定值．

【题目】在直角坐标系xOy中，直线l的参数方程为 （t为参数）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C：ρ=2 cos（θ﹣ ）．
（Ⅰ） 求直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ） 求曲线C上的点到直线l的距离的最大值．

【题目】已知在 的展开式中，第6项为常数项．
（Ⅰ）求含x2的项的系数；
（Ⅱ）求展开式中所有的有理项．

【题目】若函数f(x)满足：对于s，t∈[0，+∞），都有f(s)≥0，f(t)≥0，且f(s)+f(t)≤f(s+t)，则称函数f (x)为“T函数”．

(I)试判断函数f1(x)=x2与f2(x)=lg(x+1)是否是“T函数”，并说明理由；

(Ⅱ)设f (x)为“T函数”，且存在x0∈[0，+∞)，使f(f(x0))=x0.求证：f (x0) =x0；

(Ⅲ)试写出一个“T函数”f(x)，满足f(1)=1，且使集合{y|y=f(x)，0≤x≤1)中元素的个数最少．（只需写出结论）

【题目】如图，四面体中， 平面， ， ， ， .

（Ⅰ）求四面体的四个面的面积中，最大的面积是多少？

（Ⅱ）证明：在线段上存在点，使得，并求的值．

【题目】命题p：关于x的方程x2+ax+2=0无实根，命题q：函数f（x）=logax在（0，+∞）上单调递增，若“p∧q”为假命题，“p∨q”真命题，求实数a的取值范围．

【题目】已知函数对任意实数均有，其中常数为负数，且在区间上有表达式.

(1)写出在上的表达式，并写出函数在上的单调区间(不用过程，直接写出即可)；

(2)求出在上的最小值与最大值，并求出相应的自变量的取值.

【题目】李庄村某社区电费收取有以下两种方案供农户选择：

方案一：每户每月收管理费2元，月用电不超过30度，每度0.4元，超过30度时，超过部分按每度0.5元.

方案二：不收管理费，每度0.48元.

（1）求方案一收费元与用电量（度）间的函数关系；

（2）小李家九月份按方案一交费34元，问小李家该月用电多少度？

（3）小李家月用电量在什么范围时，选择方案一比选择方案二更好？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网