题目内容
(12分)设 =(4,-3),
=(4,-3), =(2,1),是否存在实数t,使得
=(2,1),是否存在实数t,使得 +t
+t 与
与 的夹角为45º.若存在,求出t的值,若不存在说明理由.
的夹角为45º.若存在,求出t的值,若不存在说明理由.
 =(4,-3),
=(4,-3), =(2,1),是否存在实数t,使得
=(2,1),是否存在实数t,使得 +t
+t 与
与 的夹角为45º.若存在,求出t的值,若不存在说明理由.
的夹角为45º.若存在,求出t的值,若不存在说明理由. 1
假设存在实数t,使得 +t
+t 与
与 的夹角为45º,
的夹角为45º,
由于 +t
+t =(-4,3)+t(2,1)=(4+2t,t-3),
=(-4,3)+t(2,1)=(4+2t,t-3),
( +t
+t )·
)· =(4+2t,t-3)·(2,1)=5t+5,
=(4+2t,t-3)·(2,1)=5t+5,
则| +t
+t |=
|=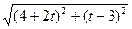 =
=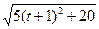 ,
,
而( +t
+t )·
)· =|
=| +t
+t |·|
|·| |cos45º,即5t+5=
|cos45º,即5t+5=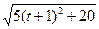 ×
×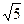 ×
×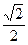 ,
,
得t2+2t-3=0,∴t=-3或t=1,经检验知t=-3不合题意,故舍去,
∴存在实数t=1,使得 +t
+t 与
与 的夹角为45º.
的夹角为45º.
 +t
+t 与
与 的夹角为45º,
的夹角为45º,由于
 +t
+t =(-4,3)+t(2,1)=(4+2t,t-3),
=(-4,3)+t(2,1)=(4+2t,t-3),(
 +t
+t )·
)· =(4+2t,t-3)·(2,1)=5t+5,
=(4+2t,t-3)·(2,1)=5t+5,则|
 +t
+t |=
|=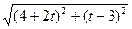 =
=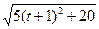 ,
,而(
 +t
+t )·
)· =|
=| +t
+t |·|
|·| |cos45º,即5t+5=
|cos45º,即5t+5=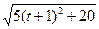 ×
×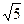 ×
×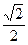 ,
,得t2+2t-3=0,∴t=-3或t=1,经检验知t=-3不合题意,故舍去,
∴存在实数t=1,使得
 +t
+t 与
与 的夹角为45º.
的夹角为45º.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,动点
,动点 、
、 分别在
分别在 、
、 轴上运动,满足
轴上运动,满足 ,
, 为动点,并且满足
为动点,并且满足 .
. 的方程;
的方程; 的直线
的直线 (不与
(不与 两点,设点
两点,设点  ,
, 与
与 的夹角为
的夹角为 ,求证:
,求证: .
.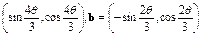 ,且
,且 ∈
∈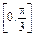 .
.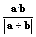 的最值;
的最值;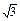 |a-kb| (k∈R),求k的取值范围.
|a-kb| (k∈R),求k的取值范围. C所在平面内的一点,
C所在平面内的一点,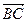 +
+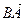 =2
=2 ,则 ( )
,则 ( ) +
+ =
=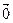
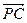 +
+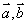 ,下列命题中错误的是( )
,下列命题中错误的是( )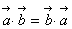
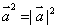
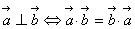
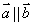
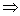
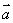 在
在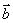 上的投影为
上的投影为
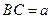 ,若长为
,若长为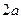
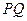 以点
以点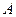 为中点,问
为中点,问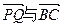 的夹角
的夹角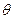 取何值时
取何值时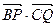 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。 ,向量
,向量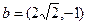 ,求
,求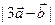 的最大值和最小值。
的最大值和最小值。