题目内容
已知a=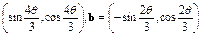 ,且
,且 ∈
∈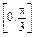 .
.
(1)求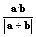 的最值;
的最值;
(2)若|ka+b|=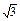 |a-kb| (k∈R),求k的取值范围.
|a-kb| (k∈R),求k的取值范围.
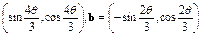 ,且
,且 ∈
∈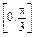 .
.(1)求
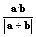 的最值;
的最值;(2)若|ka+b|=
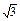 |a-kb| (k∈R),求k的取值范围.
|a-kb| (k∈R),求k的取值范围.(1)最大值为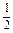 ,最小值为-
,最小值为-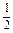 (2)k∈[2-
(2)k∈[2-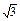 ,2+
,2+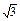 ]
]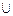 {-1}
{-1}
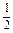 ,最小值为-
,最小值为-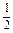 (2)k∈[2-
(2)k∈[2-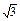 ,2+
,2+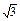 ]
]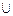 {-1}
{-1}(1)a·b=-sin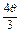 ·sin
·sin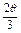 +cos
+cos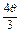 ·cos
·cos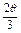 =cos2
=cos2 ,
,
|a+b|2=|a|2+|b|2+2a·b=2+2cos2 =4cos2
=4cos2 .
.
∵ ∈
∈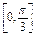 ,∴cos
,∴cos ∈
∈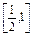 ,∴|a+b|=2cos
,∴|a+b|=2cos .
.
∴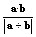 =
= 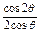 =cos
=cos -
-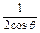 .
.
令t=cos ,则
,则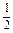 ≤t≤1,
≤t≤1,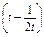 ′=1+
′=1+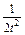 >0,
>0,
∴t-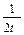 在t∈
在t∈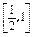 上为增函数.
上为增函数.
∴-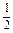 ≤t-
≤t-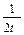 ≤
≤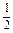 ,
,
即所求式子的最大值为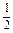 ,最小值为-
,最小值为-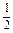 .
.
(2)由题设可得|ka+b|2=3|a-kb|2,
∴(ka+b)2=3(a-kb)2
又|a|=|b|=1,a·b=cos2 ,∴cos2
,∴cos2 =
=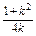 .
.
由 ∈
∈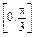 ,得-
,得-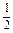 ≤cos2
≤cos2 ≤1.
≤1.
∴-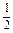 ≤
≤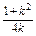 ≤1.解得k∈[2-
≤1.解得k∈[2-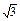 ,2+
,2+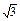 ]
]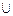 {-1}.
{-1}.
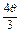 ·sin
·sin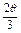 +cos
+cos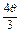 ·cos
·cos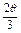 =cos2
=cos2 ,
,|a+b|2=|a|2+|b|2+2a·b=2+2cos2
 =4cos2
=4cos2 .
.∵
 ∈
∈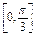 ,∴cos
,∴cos ∈
∈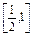 ,∴|a+b|=2cos
,∴|a+b|=2cos .
.∴
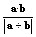 =
= 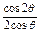 =cos
=cos -
-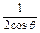 .
.令t=cos
 ,则
,则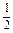 ≤t≤1,
≤t≤1,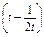 ′=1+
′=1+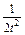 >0,
>0,∴t-
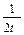 在t∈
在t∈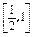 上为增函数.
上为增函数.∴-
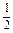 ≤t-
≤t-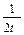 ≤
≤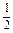 ,
,即所求式子的最大值为
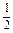 ,最小值为-
,最小值为-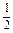 .
.(2)由题设可得|ka+b|2=3|a-kb|2,
∴(ka+b)2=3(a-kb)2
又|a|=|b|=1,a·b=cos2
 ,∴cos2
,∴cos2 =
=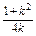 .
.由
 ∈
∈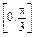 ,得-
,得-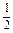 ≤cos2
≤cos2 ≤1.
≤1.∴-
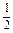 ≤
≤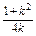 ≤1.解得k∈[2-
≤1.解得k∈[2-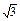 ,2+
,2+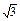 ]
]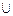 {-1}.
{-1}.
练习册系列答案
相关题目
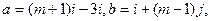 其中i,j为互相垂直的单位向量,又
其中i,j为互相垂直的单位向量,又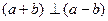 ,则实数m =( )。
,则实数m =( )。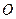
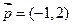
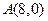
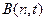
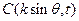
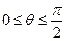
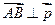 ,且
,且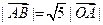 ,求向量
,求向量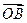 ;
;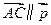 ,当
,当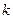 为大于4的某个常数时,
为大于4的某个常数时,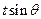 取最大值4,求此时
取最大值4,求此时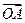 与
与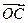 夹
夹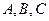 是
是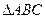 的内角,向量
的内角,向量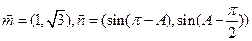 ,
,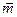 ⊥
⊥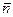 .(Ⅰ)求角A的大小;(Ⅱ)求函数
.(Ⅰ)求角A的大小;(Ⅱ)求函数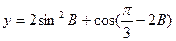 的值域.
的值域.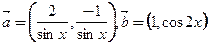 且
且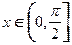 ,(Ⅰ)若
,(Ⅰ)若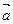 与
与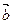 是两个共线向量,求
是两个共线向量,求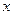 的值;
的值;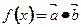 ,求函数
,求函数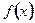 的最小值及相应的
的最小值及相应的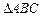 中,点
中,点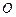 在边
在边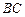 中线
中线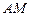 上,若
上,若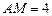 ,则
,则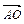 ·(
·(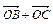 )的( )
)的( )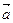 =(4,-3),
=(4,-3),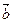 =(2,1),是否存在实数t,使得
=(2,1),是否存在实数t,使得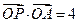 ,则点P的轨迹方程是 .
,则点P的轨迹方程是 .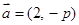 ,
,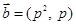 ,向量
,向量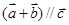 ,则
,则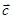 可以是
可以是 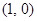 .
.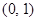 .
.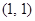 .
.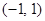 .
.