题目内容
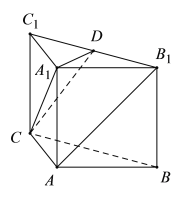
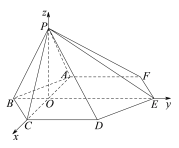
【题目】如图,在六棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正六边形,
的正六边形,![]() .
.
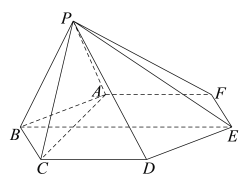
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)要证明面面垂直,需先证明线面垂直,设![]() ,连结
,连结![]() ,根据正六边形的性质和条件,可证明
,根据正六边形的性质和条件,可证明![]() 平面
平面![]() ;(2)首先证明
;(2)首先证明![]() ,即
,即![]() 、
、![]() 、
、![]() 两两互相垂直,以
两两互相垂直,以![]() 、
、![]() 、
、![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() (如下图所示),分别求平面
(如下图所示),分别求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据公式求解
,根据公式求解![]() .
.
解:(1)设![]() ,连结
,连结![]() .
.
在正六边形![]() 中,根据对称性
中,根据对称性![]() 为
为![]() 中点,
中点,
又![]() ,
,![]() ,
,
又因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)在正六边形![]() 中,
中,![]() ,
,
所以![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 、
、![]() 、
、![]() 两两互相垂直.
两两互相垂直.
以![]() 、
、![]() 、
、![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴、
轴、
![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() (如图所示).
(如图所示).
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由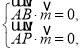 得
得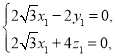 令
令![]() ,解得
,解得![]() ,
,![]() .
.
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由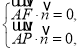 得
得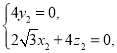 令
令![]() ,解得
,解得![]() .
.
所以![]() .
.
因此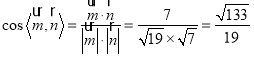 .
.
因为二面角![]() 的平面角为钝角,
的平面角为钝角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目