题目内容
已知数列{an}满足a1=2,an+1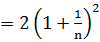 ·an(n∈N+).
·an(n∈N+).
(1)求a2,a3,并求数列{an}的通项公式.
(2)设cn= ,求证:c1+c2+c3+…+cn<
,求证:c1+c2+c3+…+cn< .
.
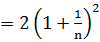 ·an(n∈N+).
·an(n∈N+).(1)求a2,a3,并求数列{an}的通项公式.
(2)设cn=
 ,求证:c1+c2+c3+…+cn<
,求证:c1+c2+c3+…+cn< .
.(1)an=n2·2n(n∈N+) (2)见解析
【解题指南】解答第(1)题的关键是根据an+1=2
 an(n∈N+)证明数列
an(n∈N+)证明数列 为等比数列.第(2)题证明的关键是选准放缩的标准.
为等比数列.第(2)题证明的关键是选准放缩的标准.解:(1)因为a1=2,an+1=2
 ·an(n∈N+),
·an(n∈N+),所以a2=2×
 ·a1=16,a3=2×
·a1=16,a3=2× ·a2=72.
·a2=72.又因为
 =2·
=2· ,n∈N+,所以
,n∈N+,所以 为等比数列.
为等比数列.所以
 =
= ·2n-1=2n,所以an=n2·2n(n∈N+).
·2n-1=2n,所以an=n2·2n(n∈N+).(2)cn=
 =
= ,
,所以c1+c2+c3+…+cn=
 +
+ +
+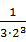 +…+
+…+ <
< +
+ +
+ +
+ ·
·
=
 +
+ ·
· <
< +
+ ·
· =
= +
+ =
= =
= <
< =
= ,所以结论成立.
,所以结论成立.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,
, ,
, 也可以构成一个三角形.
也可以构成一个三角形. 的不等式
的不等式 的解集为
的解集为 ,且
,且 个整数,则当
个整数,则当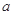 的值为______________.
的值为______________. ,若不等式
,若不等式 的解集为
的解集为 ,则实数
,则实数 的值为 .
的值为 . 对于一切实数
对于一切实数 均成立,则实数
均成立,则实数 的取值范围是______.
的取值范围是______. +
+ 取最小值时的实数对(a,b)
取最小值时的实数对(a,b) +
+
 +
+
 ,x∈
,x∈
 (x>10且x≠11)
(x>10且x≠11)