题目内容
给出下列四个命题:
(1)若函数f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,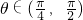 ,则f(sinθ)>f(cosθ);
,则f(sinθ)>f(cosθ);
(2)若锐角α,β满足cosα>sinβ,则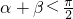 ;
;
(3)函数f(x)=sin2xcos2x的最小正周期是 ;
;
(4)要得到函数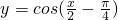 的图象,只需将y=sin
的图象,只需将y=sin 向左平移
向左平移 个单位.其中正确命题的个数为
个单位.其中正确命题的个数为
- A.1
- B.2
- C.3
- D.4
B
分析:(1)由已知可得函数在[0,1]上单调递减,结合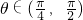 ,可知0<cosθ<sinθ<1,从而可判断(1)
,可知0<cosθ<sinθ<1,从而可判断(1)
(2)由锐角α,β满足cosα>sinβ可得sin( )>sinβ,则有
)>sinβ,则有 ,则可判断(2)
,则可判断(2)
(3)由周期公式可得,函数f(x)=sin2xcos2x= sin4x的最小正周期
sin4x的最小正周期
(4)根据函数的图象的平移法则可得,把函数y=sin 向左平移
向左平移 个单位可得y=sin[
个单位可得y=sin[ (x+
(x+ )],故可判断(4)
)],故可判断(4)
解答:(1)由函数f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,可得函数在[0,1]上单调递减,由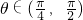 ,可得0<cosθ<sinθ<1,则f(sinθ)<f(cosθ),故(1)错误
,可得0<cosθ<sinθ<1,则f(sinθ)<f(cosθ),故(1)错误
(2)由锐角α,β满足cosα>sinβ可得sin( )>sinβ,则有
)>sinβ,则有 即
即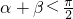 ,故(2)正确
,故(2)正确
(3)由周期公式可得,函数f(x)=sin2xcos2x= sin4x的最小正周期是
sin4x的最小正周期是 ,故(3)正确
,故(3)正确
(4)根据函数的图象的平移法则可得,把函数y=sin 向左平移
向左平移 个单位可得y=sin[
个单位可得y=sin[ (x+
(x+ )]即y=sin
)]即y=sin 的图象,故(4)错误
的图象,故(4)错误
故选:B
点评:本题主要考查了偶函数的对称区间上的单调性相反的应用,三角函数的单调性、周期的求解、函数的图象的平移法则的应用,属于三角函数知识的综合应用
分析:(1)由已知可得函数在[0,1]上单调递减,结合
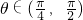 ,可知0<cosθ<sinθ<1,从而可判断(1)
,可知0<cosθ<sinθ<1,从而可判断(1)(2)由锐角α,β满足cosα>sinβ可得sin(
 )>sinβ,则有
)>sinβ,则有 ,则可判断(2)
,则可判断(2)(3)由周期公式可得,函数f(x)=sin2xcos2x=
 sin4x的最小正周期
sin4x的最小正周期(4)根据函数的图象的平移法则可得,把函数y=sin
 向左平移
向左平移 个单位可得y=sin[
个单位可得y=sin[ (x+
(x+ )],故可判断(4)
)],故可判断(4)解答:(1)由函数f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,可得函数在[0,1]上单调递减,由
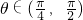 ,可得0<cosθ<sinθ<1,则f(sinθ)<f(cosθ),故(1)错误
,可得0<cosθ<sinθ<1,则f(sinθ)<f(cosθ),故(1)错误(2)由锐角α,β满足cosα>sinβ可得sin(
 )>sinβ,则有
)>sinβ,则有 即
即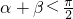 ,故(2)正确
,故(2)正确(3)由周期公式可得,函数f(x)=sin2xcos2x=
 sin4x的最小正周期是
sin4x的最小正周期是 ,故(3)正确
,故(3)正确(4)根据函数的图象的平移法则可得,把函数y=sin
 向左平移
向左平移 个单位可得y=sin[
个单位可得y=sin[ (x+
(x+ )]即y=sin
)]即y=sin 的图象,故(4)错误
的图象,故(4)错误故选:B
点评:本题主要考查了偶函数的对称区间上的单调性相反的应用,三角函数的单调性、周期的求解、函数的图象的平移法则的应用,属于三角函数知识的综合应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目