题目内容
已知椭圆![]() 的离心率为
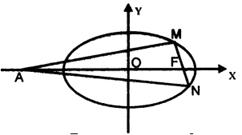
的离心率为![]() ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且![]() ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当![]() 时.,
时.,![]() ;
;
(2)若当![]() 时有
时有![]() ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当![]() 的值为6
的值为6![]() 时, 求出直线MN的方程.
时, 求出直线MN的方程.
(1)见解析
(2)椭圆C的方程为![]()
(3)直线的MN方程为![]() ,或
,或![]() 。
。
解析:
(1)设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
由M,N两点在椭圆上,![]()
若![]() ,则
,则![]() (舍去),
(舍去),![]() (4分)
(4分)
![]() 。(5分)
。(5分)
(2)当![]() 时,不妨设
时,不妨设![]() (6分)
(6分)
又![]() ,
,![]() , (8分)
, (8分)
椭圆C的方程为![]() 。 (9分)
。 (9分)
(3)因为![]() =6
=6![]() , (10分)
, (10分)
由(2)知点F(2,0), 所以|AF|=6, 即得|yM-yN|=![]() (11分)
(11分)
当MN⊥x轴时, |yM-yN|=|MN|=![]() , 故直线MN的斜率存在, (12分)
, 故直线MN的斜率存在, (12分)
不妨设直线MN的方程为![]()
联立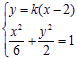 ,得
,得![]() ,
,
![]() =
=![]() , 解得k=±1。
, 解得k=±1。
此时,直线的MN方程为![]() ,或
,或![]() 。 (14分)
。 (14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: