题目内容
设Sn是等差数列{an}的前n项和,若a2=2,S4=14,则公差d等于( )
| A.2 | B.3 | C.4 | D.5 |
由等差数列的通项公式可得a2=a1+d=2,即a1=2-d,①
由等差数列的求和公式可得S4=4a1+
d=14,②
把①代入②可得4(2-d)+6d=14,解得d=3
故选:B
由等差数列的求和公式可得S4=4a1+
| 4×3 |
| 2 |
把①代入②可得4(2-d)+6d=14,解得d=3
故选:B

练习册系列答案
相关题目
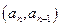 在直线
在直线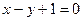 上,
上, 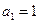 ,
,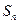 是数列
是数列 的前n项和,数列
的前n项和,数列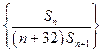 的最大值为
的最大值为