题目内容
6.两直线3x-4y-3=0和6x-8y+19=0之间的距离为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
分析 两条平行直线即即两直线6x-8y-6=0和6x-8y+19=0,由此利用两平行线间的距离公式求得它们间的距离.
解答 解:两直线3x-4y-3=0和6x-8y+19=0,即两直线6x-8y-6=0和6x-8y+19=0,
故它们之间的距离为 $\frac{|-6-19|}{\sqrt{36+64}}$=$\frac{5}{2}$,
故选:C.
点评 本题主要考查两平行线间的距离公式的应用,要注意先把两直线的方程中x,y的系数化为相同的,然后才能用两平行线间的距离公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知O是△ABC内部一点,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,$\overrightarrow{AB}$•$\overrightarrow{AC}$=6,∠BAC=60°,则△OBC的面积为( )
| A. | 3$\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 3 |
17.在三棱锥P-ABC中,$\overrightarrow{PA}=\vec a$,$\overrightarrow{PB}=\vec b$,$\overrightarrow{PC}=\vec c$,E为棱AB的中点,则$\overrightarrow{CE}$等于( )
| A. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\vec a+\vec b-\frac{1}{2}\vec c$ | C. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\vec c$ | D. | $\frac{1}{2}\vec a+\vec b-\frac{1}{2}\vec c$ |
15.关于x的方程x2-2x+5=0的一个根是1-2i,则另一根的虚部为( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
16.运行如图所示的程序框图,则输出k的值是( )
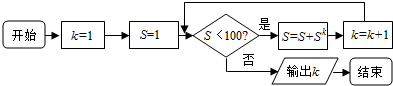

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |