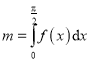��Ŀ����
����Ŀ��Ϊ�����ļ����ºͶ�����ůʱ������Դ��ģ����ݵ��ݶ�����ǽ��Ҫ������Ȳ㣮ij��������Ҫ�����ʹ��20��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ6��Ԫ���ý�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��= ![]() ��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
��1����k��ֵ��f��x���ı���ʽ��
��2�����Ȳ������ʱ���ܷ���f��x���ﵽ��С��������Сֵ��
���𰸡�
��1���⣺����Ȳ���Ϊxcm�������裬ÿ����Դ���ķ���Ϊ ![]() ��
��
����C��0��=8����k=40��
��� ![]() ��
��
���������ΪC1��x��=6x��
���ø��Ȳ㽨�������20�����Դ���ķ���֮��Ϊ
![]()
��2���⣺ ![]() ����f'��x��=0����
����f'��x��=0���� ![]() ��
��
���x=5�� ![]() ����ȥ����
����ȥ����
��0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ ![]() ��
��
�����Ȳ���5cm��ʱ���ܷ��ôﵽ��СֵΪ70��Ԫ
����������1���ɽ�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��= ![]() �����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ�����ǿɵ�C��0��=8����k=40�������õ�
�����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ�����ǿɵ�C��0��=8����k=40�������õ� ![]() ���������ΪC1��x��=6x������ݸ��Ȳ㽨�������20�����Դ���ķ���֮��Ϊf��x�������Dz��ѵõ�f��x���ı���ʽ����2���ɣ�1���������f��x���ı���ʽ���������õ��������������f��x���ĵ����ԣ�Ȼ����ݺ���������������ܷ���f��x������Сֵ��
���������ΪC1��x��=6x������ݸ��Ȳ㽨�������20�����Դ���ķ���֮��Ϊf��x�������Dz��ѵõ�f��x���ı���ʽ����2���ɣ�1���������f��x���ı���ʽ���������õ��������������f��x���ĵ����ԣ�Ȼ����ݺ���������������ܷ���f��x������Сֵ��