题目内容
已知△ABC所在平面内有一点P,满足4
+
+
=
,则
=
.
| PA |
| BP |
| CP |
| 0 |
| S△PAB |
| S△ABC |
| 1 |
| 2 |
| 1 |
| 2 |
分析:取BC中点O,可得
=
,结合图形,可得面积的关系.
| PA |
| AO |
解答: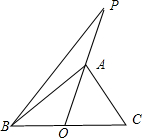 解:∵4
解:∵4
+
+
=
,
∴2
=
+
取BC中点O,则
+
=2
∴
=
∴S△PAB=S△ABO
∵S△ABO=
S△ABC
∴
=
故答案为:
 解:∵4
解:∵4| PA |
| BP |
| CP |
| 0 |
∴2
| PA |
| AB |
| AC |
取BC中点O,则
| AB |
| AC |
| AO |
∴
| PA |
| AO |
∴S△PAB=S△ABO
∵S△ABO=
| 1 |
| 2 |
∴
| S△PAB |
| S△ABC |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查向量知识的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
已知△ABC所在平面上的动点M满足2
•
=
2 -
2,则M点的轨迹过△ABC的( )
| AM |
| BC |
| AC |
| AB |
| A、内心 | B、垂心 | C、重心 | D、外心 |