题目内容
(理科做)已知△ABC所在平面内一点P(P与A、B、C都不重合),且满足
+
+
=
,则△ACP与△BCP的面积之比为
| PA |
| PB |
| PC |
| BC |
2
2
.分析:利用向量的运算法则将等式变形,据三点共线的充要条件得出结论,推出P为经过三等分点,△PBC与△PAB的底边边长与高乘积之比,进而得到△PBC与△PAB的面积之比.
解答: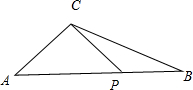 解:∵
解:∵
+
+
=
,∴
+
=
+
∴
=2
,
∴P是AB边的一个三等分点.如图
所以△ACP与△BCP的底边的比为2,C到AB的距离相等,所以面积之比为2.
即s1:s2=2
故答案为:2.
 解:∵
解:∵| PA |
| PB |
| PC |
| BC |
| PA |
| PB |
| CP |
| BC |
| PA |
| BP |
∴P是AB边的一个三等分点.如图
所以△ACP与△BCP的底边的比为2,C到AB的距离相等,所以面积之比为2.
即s1:s2=2
故答案为:2.
点评:本题考查的知识点是平行向量与共线向量,其中根据数乘向量的几何意义,分析出表达式所表示的几何意义,即△PBC与△PAB的底边边长之比和高之比,是解答本题的关键.

练习册系列答案
相关题目