Question

（2007•汕头二模）给出以下五个命题：
①?n∈N^*，（n²-5n+5）²=1．
②当x，y满足不等式组

x≥0 x≥y 2x-y≤1

时，目标函数k=3x+2y的最大值为5．
③设全集U={1，2，3，4，5，6}，集合A={3，4}，B={3，6}，则?_U（A∪B）={1，2，3，5，6}．
④定义在R上的函数y=f（x）在区间（1，2）上存在唯一零点的充要条件是f（1）•f（2）＜0．
⑤已知△ABC所在平面内一点P（P与A，B，C都不重合）满足

PA

+

PB

+

PC

=

BC

，则△ACP与△BCP的面积之比为2．
其中正确命题的序号是

②⑤

．

Answer 1

分析：①利用全称命题的性质判断．②利用线性规划进行判断．③利用集合的基本运算进行判断．④利用根的存在定理进行判断．⑤利用向量的应用判断．

解答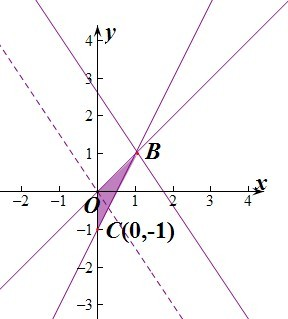：解：①中，n=5时（n²-5n+5）²=（5²-5×5+5）²=5²=25≠1不成立，所以①错误；
②由k=3x+2y得y=-

3

2

x+

k

2

，画出可行域，平移直线y=-

3

2

x+

k

2

，由平移可知当直线y=-

3

2

x+

k

2

，经过点B时，直线y=-

3

2

x+

k

2

的截距最大，此时k最大．
由

x-y=0 2x-y=1

，得

x=1 y=1

，即B（1，1），代入k=3x+2y得k=3+2=5，即目标函数k=3x+2y的最大值为5，所以②正确；
③因为A={3，4}，B={3，6}，所以A∪B={3，4，6}，所以C_U（A∪B）={1，2，5}，所以③错误；
④根据根的存在性定理可知若f（1）•f（2）＜0，此时零点不唯一，所以④错误；
⑤

PA

+

PB

+

PC

=

BC

=

PC

-

PB

所以

PA

=-2

PB

，则△ACP与△BCP的面积之比为2，
所以⑤正确．
故答案为：②⑤．

点评：本题主要考查各种命题的真假判断，综合性较强．