题目内容
设α∈(0,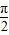 ),函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,对定义域内任意的x,y,满足f(
),函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,对定义域内任意的x,y,满足f(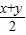 )=f(x)sinα+(1-sinα)f(y),求:
)=f(x)sinα+(1-sinα)f(y),求:(1)f(
 )及sinα的值;
)及sinα的值;(2)函数g(x)=sin(α-2x)的单调递增区间;
(3)(理)n∈N时,an=
 ,求f(an),并猜测x∈[0,1]时,f(x)的表达式(不需证明).
,求f(an),并猜测x∈[0,1]时,f(x)的表达式(不需证明).
【答案】分析:(1)分别取x=1,y=0与x=0,y=1,求出sinα的值,从而求出f( )的值;
)的值;
(2)先求出α,然后根据正弦函数的单调区间求出该函数的单调区间,将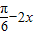 看成整体进行求解即可;
看成整体进行求解即可;
(3)根据条件可得f(an)是首项为f(a1)= ,公比为
,公比为 的等比数列,即可猜测:f(x)=x.
的等比数列,即可猜测:f(x)=x.
解答:解:(1)f( )=f(1)sinα+(1-sinα)f(0)=sinα,
)=f(1)sinα+(1-sinα)f(0)=sinα,
又:f( )=f(0)sinα+(1-sinα)f(1)=1-sinα,
)=f(0)sinα+(1-sinα)f(1)=1-sinα,
∴sinα=1-sinα⇒sinα=
∴f( )=1-
)=1- =
=
(2)由(1)知:sinα= ,又α∈(0,
,又α∈(0,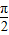 )
)
∴α=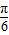
∴g(x)=sin(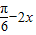 ),
),
∴g(x)的增区间为[kπ-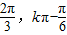 ](k∈Z).
](k∈Z).
(3)∵n∈N,an=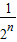 ,f(an)=f(
,f(an)=f(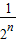 )(n∈N,n≥2)
)(n∈N,n≥2)
∴f(an)是首项为f(a1)= ,公比为
,公比为 的等比数列,故f(an)=f(a1)•qn-1′=
的等比数列,故f(an)=f(a1)•qn-1′=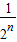 ,猜测:f(x)=x.
,猜测:f(x)=x.
点评:本题主要考查了正弦函数的单调性,以及数列与函数的综合,同时考查了计算能力,属于中档题.
 )的值;
)的值;(2)先求出α,然后根据正弦函数的单调区间求出该函数的单调区间,将
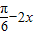 看成整体进行求解即可;
看成整体进行求解即可;(3)根据条件可得f(an)是首项为f(a1)=
 ,公比为
,公比为 的等比数列,即可猜测:f(x)=x.
的等比数列,即可猜测:f(x)=x.解答:解:(1)f(
 )=f(1)sinα+(1-sinα)f(0)=sinα,
)=f(1)sinα+(1-sinα)f(0)=sinα,又:f(
 )=f(0)sinα+(1-sinα)f(1)=1-sinα,
)=f(0)sinα+(1-sinα)f(1)=1-sinα,∴sinα=1-sinα⇒sinα=

∴f(
 )=1-
)=1- =
=
(2)由(1)知:sinα=
 ,又α∈(0,
,又α∈(0,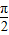 )
)∴α=
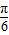
∴g(x)=sin(
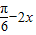 ),
),∴g(x)的增区间为[kπ-
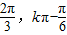 ](k∈Z).
](k∈Z).(3)∵n∈N,an=
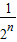 ,f(an)=f(
,f(an)=f(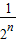 )(n∈N,n≥2)
)(n∈N,n≥2)∴f(an)是首项为f(a1)=
 ,公比为
,公比为 的等比数列,故f(an)=f(a1)•qn-1′=
的等比数列,故f(an)=f(a1)•qn-1′=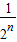 ,猜测:f(x)=x.
,猜测:f(x)=x.点评:本题主要考查了正弦函数的单调性,以及数列与函数的综合,同时考查了计算能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
设abc>0,二次函数f(x)=ax2+bx+c的图象可能是( )
A、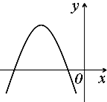 | B、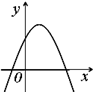 | C、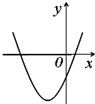 | D、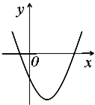 |
设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为( )
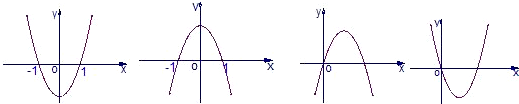

| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、
|
