题目内容
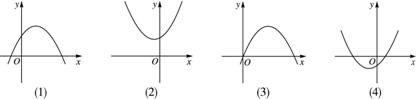
设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为( )
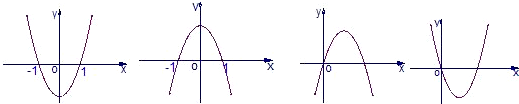

| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、
|
分析:根据题中条件可先排除前两个图形,然后根据后两个图象都经过原点可求出a的两个值,再根据抛物线的开口方向就可确定a的值
解答:解:∵b>0
∴抛物线对称轴不能为y轴,
∴可排除掉前两个图象.
∵剩下两个图象都经过原点,
∴a2-1=0,
∴a=±1.
∵当a=1时,抛物线开口向上,对称轴在y轴左方,
∴第四个图象也不对,
∴a=-1,
故选B.
∴抛物线对称轴不能为y轴,
∴可排除掉前两个图象.
∵剩下两个图象都经过原点,
∴a2-1=0,
∴a=±1.
∵当a=1时,抛物线开口向上,对称轴在y轴左方,
∴第四个图象也不对,
∴a=-1,
故选B.
点评:本题考查了抛物线的图形和性质,做题时注意题中条件的利用.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目