题目内容
已知椭圆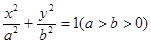
的右焦点为
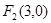，离心率为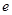
.
(1)若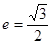
,求椭圆的方程; (2)设直线
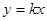与椭圆相交于
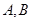两点,
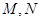分别为线段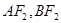
的中点.若坐标原点
在以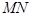
为直径的圆上,且
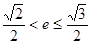,求
的取值范围.
（1）椭圆方程：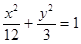
（2）
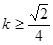或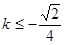
解析
练习册系列答案
同步练习强化拓展系列答案
相关题目
同步练习强化拓展系列答案题目内容
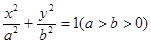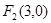已知椭圆的右焦点为，离心率为.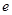
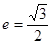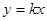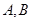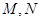(1)若,求椭圆的方程; (2)设直线与椭圆相交于两点,分别为线段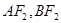的中点.若坐标原点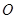在以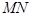为直径的圆上,且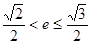,求的取值范围.
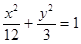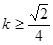（1）椭圆方程： （2）或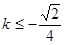
解析
同步练习强化拓展系列答案
.过点
作圆
的切线
交椭圆
于
，
两点.
表示为
的函数，并求
的离心率
，过右焦点
的直线
与椭圆
相交于
两点，当直线
到直线
.
，使得当直线
成立？若存在，求出所有满足条件的点
:
的两个焦点为
,点
在椭圆
.
过圆
的圆心，交椭圆
两点，且
对称，求直线
的长轴为
，过点
的直线
与
轴垂直，直线
所经过的定点恰好是椭圆的一个顶点，且椭圆的离心率
是椭圆上异于
、
轴，
为垂足，延长
到点
使得
，连接
并延长交直线
，
为
的中点．试判断直线
与以
的位置关系．
经过点
，一个焦点是
．
的方程；
轴的两个交点为
、
，点
在直线
上，直线
、
分别与椭圆
、
两点．试问：当点
是否恒经过定点
？证明你的结论．
中，
是抛物线
的焦点，
是抛物线
上位于第一象限内的任意一点，过
三点的圆的圆心为
，点
．（Ⅰ）求抛物线
与抛物线
若存在，求出点
与坐标轴的交点都在圆上．
交于A，B两点，且
求a的值． 
是双曲线
上不同的三点，且
连线经过坐标原点，
的斜率乘积
，求双曲线的离心率；