题目内容
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(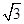 ,0).
,0).
(1)求双曲线C的方程;
(2)若直线l:y=kx+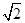 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且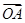 ·
·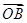 >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.
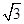 ,0).
,0).(1)求双曲线C的方程;
(2)若直线l:y=kx+
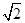 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且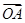 ·
·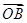 >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.(1)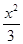 -y2=1
-y2=1
(2)(-1,-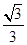 )∪(
)∪(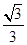 ,1)
,1)
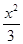 -y2=1
-y2=1(2)(-1,-
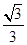 )∪(
)∪(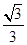 ,1)
,1)(1)设双曲线C的方程为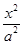 -
-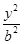 =1(a>0,b>0).
=1(a>0,b>0).
由已知得a=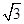 ,c=2,再由c2=a2+b2得b2=1,
,c=2,再由c2=a2+b2得b2=1,
所以双曲线C的方程为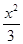 -y2=1.
-y2=1.
(2)将y=kx+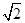 代入
代入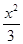 -y2=1中,整理得(1-3k2)x2-6
-y2=1中,整理得(1-3k2)x2-6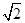 kx-9=0,
kx-9=0,
由题意得
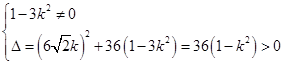 ,
,
故k2≠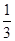 且k2<1 ①.
且k2<1 ①.
设A(xA,yA),B(xB,yB),则xA+xB= ,xAxB=
,xAxB=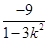 ,
,
由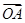 ·
·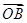 >2得xAxB+yAyB>2,
>2得xAxB+yAyB>2,
xAxB+yAyB=xAxB+(kxA+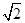 )(kxB+
)(kxB+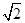 )=(k2+1)xAxB+
)=(k2+1)xAxB+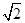 k(xA+xB)+2=(k2+1)·
k(xA+xB)+2=(k2+1)·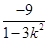 +
+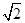 k·
k· +2=
+2=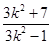 ,
,
于是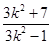 >2,即
>2,即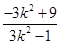 >0,解得
>0,解得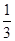 <k2<3 ②.
<k2<3 ②.
由①②得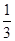 <k2<1,
<k2<1,
所以k的取值范围为(-1,-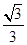 )∪(
)∪(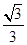 ,1).
,1).
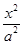 -
-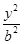 =1(a>0,b>0).
=1(a>0,b>0).由已知得a=
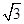 ,c=2,再由c2=a2+b2得b2=1,
,c=2,再由c2=a2+b2得b2=1,所以双曲线C的方程为
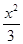 -y2=1.
-y2=1.(2)将y=kx+
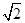 代入
代入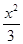 -y2=1中,整理得(1-3k2)x2-6
-y2=1中,整理得(1-3k2)x2-6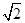 kx-9=0,
kx-9=0,由题意得
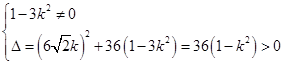 ,
,故k2≠
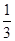 且k2<1 ①.
且k2<1 ①.设A(xA,yA),B(xB,yB),则xA+xB=
 ,xAxB=
,xAxB=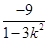 ,
,由
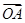 ·
·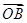 >2得xAxB+yAyB>2,
>2得xAxB+yAyB>2,xAxB+yAyB=xAxB+(kxA+
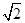 )(kxB+
)(kxB+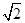 )=(k2+1)xAxB+
)=(k2+1)xAxB+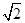 k(xA+xB)+2=(k2+1)·
k(xA+xB)+2=(k2+1)·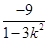 +
+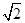 k·
k· +2=
+2=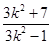 ,
,于是
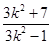 >2,即
>2,即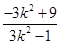 >0,解得
>0,解得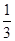 <k2<3 ②.
<k2<3 ②.由①②得
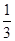 <k2<1,
<k2<1,所以k的取值范围为(-1,-
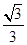 )∪(
)∪(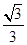 ,1).
,1).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
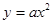 的焦点为
的焦点为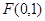 ,则
,则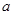 的值为( )
的值为( ) 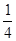
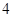
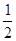
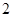
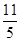
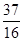
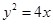 的准线方程为________.
的准线方程为________.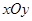 中,点
中,点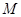 到点
到点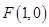 的距离比它到
的距离比它到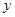 轴的距离多1,记点
轴的距离多1,记点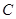 .
.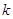 的直线
的直线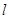 过定点
过定点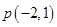 ,求直线
,求直线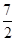 ,4),则|PA|+|PM|的最小值是( )
,4),则|PA|+|PM|的最小值是( )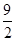
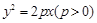 的焦点为
的焦点为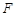 ,点
,点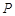 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,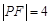 .
.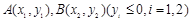 是抛物线上的两点,
是抛物线上的两点,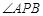 的角平分线与
的角平分线与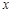 轴垂直,求
轴垂直,求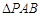 的面积最大时直线
的面积最大时直线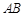 的方程.
的方程.