题目内容
(2011•孝感模拟)n2(n≥4)个正数排成行列的数表:a11、a12 、a13、…a1n,a21、a22、a23…a2n…an1、an2、an3…ann,其中,每一行数成等差数列,每一列数成等比数列,并且各列的公比都相等.已知a12=1,a14=2,a23=
,则a21=
;ann=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
n(
)n
| 1 |
| 2 |
n(
)n
.| 1 |
| 2 |
分析:因为每一行数成等差数列,每一列数成等比数列,并且各列的公比都相等.所以先根据a12=1,a14=2,a23=
,求出等差数列的公差与等比数列的公比,再根据a12=1,a14=2,a23=
,求出a21,ann.
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:∵a11、a12 、a13、…a1n成等差数列,且a12=1,a14=2
∴d=
=
,a11=a12-
=
,a13=a12+
=
,a1n=
+(n-1)×
=
∵a13,a23,a33,…,an3成等比数列,且a13=
,a23=
,∴q=
∵a11,a21,a31,…,an1成等比数列,公比为
,∴a21=a11q=
×
=
∵a1n,a2n,a3n,…,ann成等比数列,公比为
,∴ann=a1nqn-1=
(
)2=n(
)n
故答案为
,n(
)n.
∴d=
| 2-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∵a13,a23,a33,…,an3成等比数列,且a13=
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
∵a11,a21,a31,…,an1成等比数列,公比为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵a1n,a2n,a3n,…,ann成等比数列,公比为
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查了等差数列与等比数列的通项公式的应用.

练习册系列答案
相关题目
 (2011•孝感模拟)已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( )
(2011•孝感模拟)已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( )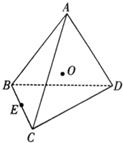 (2011•孝感模拟)如图,正四面体ABCD的外接球球心为D,E是BC的中点,则直线OE与平面BCD所成角的正切值为
(2011•孝感模拟)如图,正四面体ABCD的外接球球心为D,E是BC的中点,则直线OE与平面BCD所成角的正切值为