题目内容
(2012•肇庆二模)已知点P是圆F1:(x+
)2+y2=16上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点.
(1)求点M的轨迹C的方程;
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连接AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点.试判断直线QN与以AB为直径的圆O的位置关系.
| 3 |
(1)求点M的轨迹C的方程;
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连接AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点.试判断直线QN与以AB为直径的圆O的位置关系.
分析:(1)先确定F1、F2的坐标,再根据线段PF2的中垂线与PF1交于M点,结合椭圆的定义,可得点M的轨迹是以F1、F2为焦点的椭圆,从而可得点M的轨迹C的方程;
(2)先确定Q点在以AB为直径的圆O上,再验证
•
=0,即可知直线QN与圆O相切.
(2)先确定Q点在以AB为直径的圆O上,再验证
| OQ |
| NQ |
解答: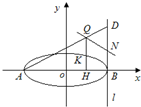 解:(1)由题意得,F1(-
解:(1)由题意得,F1(-
,0),F2(
,0)(1分)
圆F1的半径为4,且|MF2|=|MP|(2分)
从而|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|=2
(3分)
∴点M的轨迹是以F1、F2为焦点的椭圆,其中长轴2a=4,焦距2c=2
,
则短半轴b=
=
=1,(4分)
椭圆方程为:
+y2=1(5分)
(2)设K(x0,y0),则
+y02=1.
∵HK=KQ,∴Q(x0,2y0).∴OQ=
=2(6分)
∴Q点在以O为圆心,2为半径的圆上.即Q点在以AB为直径的圆O上.(7分)
又A(-2,0),∴直线AQ的方程为y=
(x+2). (8分)
令x=2,得D(2,
). (9分)
又B(2,0),N为DB的中点,∴N(2,
). (10分)
∴
=(x0,2y0),
=(x0-2,
). (11分)
∴
•
=x0(x0-2)+2y0•
=x0(x0-2)+
=x0(x0-2)+
=x0(x0-2)+x0(2-x0)=0. (13分)
∴
⊥
.∴直线QN与圆O相切.(14分)
 解:(1)由题意得,F1(-
解:(1)由题意得,F1(-| 3 |
| 3 |
圆F1的半径为4,且|MF2|=|MP|(2分)
从而|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|=2
| 3 |
∴点M的轨迹是以F1、F2为焦点的椭圆,其中长轴2a=4,焦距2c=2
| 3 |
则短半轴b=
| a2-c2 |
| 4-3 |
椭圆方程为:
| x2 |
| 4 |
(2)设K(x0,y0),则
| x02 |
| 4 |
∵HK=KQ,∴Q(x0,2y0).∴OQ=
| x02+(2y02) |
∴Q点在以O为圆心,2为半径的圆上.即Q点在以AB为直径的圆O上.(7分)
又A(-2,0),∴直线AQ的方程为y=
| 2y0 |
| x0+2 |
令x=2,得D(2,
| 8y0 |
| x0+2 |
又B(2,0),N为DB的中点,∴N(2,
| 4y0 |
| x0+2 |
∴
| OQ |
| NQ |
| 2x0y0 |
| x0+2 |
∴
| OQ |
| NQ |
| 2x0y0 |
| x0+2 |
| 4x0y02 |
| x0+2 |
| x0(4-x02) |
| x0+2 |
=x0(x0-2)+x0(2-x0)=0. (13分)
∴
| OQ |
| NQ |
点评:本题以圆的方程为载体,考查椭圆的定义与标准方程,考查直线与圆的位置关系,解题的关键是利用椭圆的定义判断轨迹的类型,利用向量的数量积为0,判断直线QN与圆O相切.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 (2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).
(2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).