题目内容
从集合{1,2,3,4,5}的所有非空子集中,等可能地取出一个.(Ⅰ)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(Ⅱ)记所取出的非空子集的元素个数为ξ,求ξ的分布列和数学期望Eξ
【答案】分析:(1)集合{1,2,3,4,5}的所有非空子集有25-1个,等可能地取出一个有31种结果,而满足条件集合中的所有元素之和为10的通过列举有3个,根据古典概型公式得到结果.
(2)所取出的非空子集的元素个数为ξ,由题意知ξ的可能取值是1、2、3、4、5,类似于第一问得到各值对应的概率,写出分布列,算出期望.
解答:解:记“所取出的非空子集满足性质r”为事件A
基本事件数是C51+C52+C53+C54+1=31
事件A包含的事件是{1、4、5},{2、3、5},{1、2、3、4}
∴P(A)=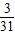 ,
,
(2)由题意知ξ的可能取值是1、2、3、4、5,
ξ的分布列是:
又P(ξ=1)=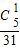 =
=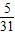 ,
,
P(ξ=2)=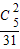 =
=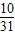 ,
,
P(ξ=3)=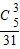 =
=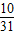
P(ξ=4)=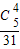 =
=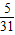
P(ξ=5)=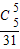 =
=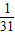
∴Eξ=1×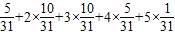 =
=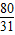
点评:本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.本题还考到了集合的子集个数问题,一个含有n个元素的集合的子集个数是2n.
(2)所取出的非空子集的元素个数为ξ,由题意知ξ的可能取值是1、2、3、4、5,类似于第一问得到各值对应的概率,写出分布列,算出期望.
解答:解:记“所取出的非空子集满足性质r”为事件A
基本事件数是C51+C52+C53+C54+1=31
事件A包含的事件是{1、4、5},{2、3、5},{1、2、3、4}
∴P(A)=
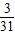 ,
,(2)由题意知ξ的可能取值是1、2、3、4、5,
ξ的分布列是:
又P(ξ=1)=
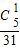 =
=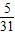 ,
,P(ξ=2)=
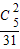 =
=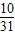 ,
,P(ξ=3)=
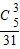 =
=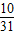
P(ξ=4)=
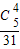 =
=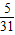
P(ξ=5)=
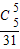 =
=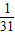
∴Eξ=1×
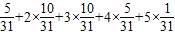 =
=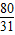
点评:本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.本题还考到了集合的子集个数问题,一个含有n个元素的集合的子集个数是2n.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
