题目内容
从集合{-1,1,2,3}中随机选取一个数记为m,从集合{1,2,3}中随机选取一个数记为n,则方程
+
=1表示椭圆的概率为
.
| ||
| m |
| ||
| n |
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据题意,由分步计数原理计算m、n选取的情况数目,由椭圆的标准方程分析可得若方程
+
=1表示椭圆,必有m、n>0且m≠n;分3种情况讨论可得方程
+
=1表示椭圆的m、n的情况数目,由等可能事件的概率公式,计算可得答案.
| ||
| m |
| ||
| n |
| ||
| m |
| ||
| n |
解答:解:根据题意,m有4个数字可选,n有3个数字可选,则m、n共有4×3=12种情况,
若方程
+
=1表示椭圆,必有m、n>0且m≠n;
分析可得:当m=1,n=2、3时,②当m=2,n=1、3时,③当m=3,n=1、2时,方程
+
=1表示椭圆,共有6种情况,
则方程
+
=1表示椭圆的概率为
=
;
故答案为
.
若方程
| ||
| m |
| ||
| n |
分析可得:当m=1,n=2、3时,②当m=2,n=1、3时,③当m=3,n=1、2时,方程
| ||
| m |
| ||
| n |
则方程
| ||
| m |
| ||
| n |
| 6 |
| 12 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查等可能事件的概率、椭圆的标准方程的定义,注意椭圆的标准方程与圆的标准方程的区别.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
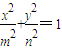 表示焦点在x轴上的椭圆的概率为 .
表示焦点在x轴上的椭圆的概率为 .