题目内容
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
解:由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
x∈A,试判断g(x)的单调性;(不证)
(3)又若B={x|
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
解:由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
| 10-x |
| 10+x |
(3)又若B={x|
| 10-x |
| 10+x |
分析:(1)先根据函数的单调性得到反函数的定义域;再求出x=-1-
即可得到函数f(x)的反函数;
(2)直接对其分离常数即可得到其单调性;
(3)先根据条件把问题转化为不等式a<
-2x+5在集合A上有解;再根据函数的单调性求出h(x)=
-2x+5在集合A上的最大值,即可得到结论.
| y-2 |
(2)直接对其分离常数即可得到其单调性;
(3)先根据条件把问题转化为不等式a<
| 10-x |
| 10+x |
| 10-x |
| 10+x |
解答:解:(1)f(x)=(x+1)2+2
∵f(x)在[-2,-1]上单调递减
∴f(x)∈[2,3]
故反函数的定义域A=[2,3](2分)
令x+1=-
,x=-1-
∴f-1(x)=-1-
x∈[2,3](4分)
(2)g(x)=
=-1+
x∈[2,3]
g(x)在x∈[2,3]上单调递减 (8分)
(3)由A∩B≠Φ,⇒不等式
>2x+a-5在集合A上有解,
亦即不等式a<
-2x+5在集合A上有解,(10分)
令函数h(x)=
-2x+5,
a<h(x)在集合A上有解,⇒a<h(x)在集合A上的最大值
又h(x)=-1+
-2x+5=
-2x+4 在区间A上单调递减
h(x)max=g(2)=
⇒a<
⇒实数a的取值范围为(-∞,
) (12分)
∵f(x)在[-2,-1]上单调递减
∴f(x)∈[2,3]
故反函数的定义域A=[2,3](2分)
令x+1=-
| y-2 |
| y-2 |
∴f-1(x)=-1-
| x-2 |
(2)g(x)=
| 10-x |
| 10+x |
| 20 |
| 10+x |
g(x)在x∈[2,3]上单调递减 (8分)
(3)由A∩B≠Φ,⇒不等式
| 10-x |
| 10+x |
亦即不等式a<
| 10-x |
| 10+x |
令函数h(x)=
| 10-x |
| 10+x |
a<h(x)在集合A上有解,⇒a<h(x)在集合A上的最大值
又h(x)=-1+
| 20 |
| 10+x |
| 20 |
| 10+x |
h(x)max=g(2)=
| 5 |
| 3 |
| 5 |
| 3 |
⇒实数a的取值范围为(-∞,
| 5 |
| 3 |
点评:本题主要考查函数的单调性的应用以及反函数的求法.是对函数知识的综合考查,属于中档题目,考查计算能力以及分析问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

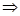 a>-2
a>-2 ,若A∩B≠
,若A∩B≠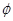 ,求实数a的取值范围.
,求实数a的取值范围.