题目内容
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x+a>0在A上有解,求实数a的取值范围.
解:令f(x)=21-x+a,因为f(x)>0在A上有解。

=2+a>0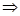 a>-2
a>-2
学习以上问题的解法,解决下面的问题,已知:函数f(x)=x2+2x+3(-2≤x≤-1).
①求f(x)的反函数f-1(x)及反函数的定义域A;
②设B=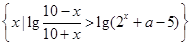 ,若A∩B≠
,若A∩B≠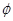 ,求实数a的取值范围.
,求实数a的取值范围.
【答案】
①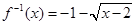 ,
,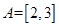 ; ②
; ②
【解析】
试题分析:①由反函数和原函数的关系可以求得反函数,求反函数的定义域时需知反函数的定义域即是原函数的值域,这样能少走好多弯路;②先由对数函数的定义和分式分母不为0求出集合B中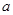 满足的不等关系,再由集合的关系及运算可以知道
满足的不等关系,再由集合的关系及运算可以知道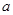 所满足的不等式,解不等式即可,解不等式是本题的重点,熟练掌握各种不等式的解法是解答本题的关键.
所满足的不等式,解不等式即可,解不等式是本题的重点,熟练掌握各种不等式的解法是解答本题的关键.
试题解析:①设 ,由反函数和原函数的关系可知,
,由反函数和原函数的关系可知,
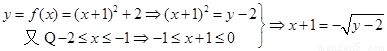 , 3分
, 3分
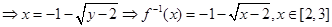 ;
6分
;
6分
②根据集合B的形式和对数函数的性质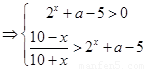 ※,
8分
※,
8分
由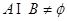 得,※在区间
得,※在区间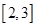 上有解,
9分
上有解,
9分
令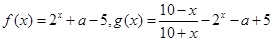 ,
,
 .
12分
.
12分
考点:反函数及其定义域的求法,集合的关系和运算,解不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目