题目内容
仔细阅读下面问题的解法:设A=[0,1],若不等式21-x+a>0在A上有解,求实数a的取值范围.解;令f(x)=21-x+a,∵f(x)>0在A上有解,∴f(x)在A上的最大值大于0.又∵f(x)在[0,1]上单调递减,
∴f(x)max=f(0)=2+a>0,∴a>-2.
学习以上问题的解法,解决下面的问题:已知函数f(x)=x2+2x+3(-2≤x≤-1).
(1)求f(x)的反函数f-1(x)及反函数的定义域A;
(2)设B={x|lg![]() >lg(2x+a-5)},若A∩B≠
>lg(2x+a-5)},若A∩B≠![]() ,求实数a的取值范围.
,求实数a的取值范围.
解:(1)y=x2+2x+3=(x+1)2+2,(x+1)2=y-2,
∵-2≤x≤-1,∴x+1=![]() ,
,
∴f-1(x)=-1-![]() ,反函数的定义域 A=[2,3].
,反函数的定义域 A=[2,3].
(2)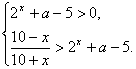 即
即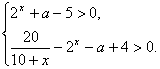
∵A∩B≠![]() ,∴不等式组在A=[2,3]上有解.
,∴不等式组在A=[2,3]上有解.
令f(x)=2x+a-5,g(x)=![]() +x-2x-a+4,
+x-2x-a+4,
易知,f(x)在A=[2,3]上单调递增;g(x)在A=[2,3]上单调递减.
则fmax=f(3)=a+3>0,∴a>-3,gmax=g(2)=![]() -a>0,∴a<
-a>0,∴a<![]() .
.
∴a∈(-3,![]() ).
).

练习册系列答案
相关题目

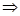 a>-2
a>-2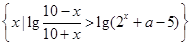 ,若A∩B≠
,若A∩B≠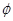 ,求实数a的取值范围.
,求实数a的取值范围.