��Ŀ����
��ϸ�Ķ���������Ľⷨ��
��A=[0, 1],������ʽ21-x-a��0��A���н�,��ʵ��a��ȡֵ��Χ��
�⣺����֪�ɵ� a �� 21-x
��f(x)= 21-x ,�߲���ʽa ��21-x��A���н�,
��a ��f(x)��A�ϵ����ֵ.
��f(x)��[0,1]�ϵ����ݼ���f(x)max =f(0)=2. ��ʵ��a��ȡֵ��ΧΪa��2.
�о�ѧϰ��������Ľⷨ��������������⣺
(1)��֪����f(x)=x2+2x+3(-2��x��-1)����f(x)�ķ��������������Ķ�����A��
(2)����(1)�е�A����g(x)=![]() ��x��A,���ж�g(x)�ĵ�����(д�����ɣ�����֤��)��
��x��A,���ж�g(x)�ĵ�����(д�����ɣ�����֤��)��
(3)��B ={x|![]() ��2x+a�C5}���Ҷ���(1)�е�A��A��B��F����ʵ��a��ȡֵ��Χ��
��2x+a�C5}���Ҷ���(1)�е�A��A��B��F����ʵ��a��ȡֵ��Χ��
��1��f-1(x)=-1-![]() x��[2,3] A=[2,3]
x��[2,3] A=[2,3]
��2��g(x)��x��[2,3]�ϵ����ݼ���3��a��ȡֵ��ΧΪ(-��,![]() ) ��
) ��
����:
(1)f(x)=(x+1)2+2
��f(x)��[-2,-1]�ϵ����ݼ���f(x)��[2,3]���ʷ������Ķ�����A=[2,3]����2��
x+1=-![]() ,x=-1-
,x=-1-![]() ��f-1(x)=-1-
��f-1(x)=-1-![]() x��[2,3] ��������4��
x��[2,3] ��������4��


��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

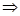 a>-2
a>-2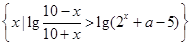 ����A��B��
����A��B��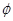 ,��ʵ��a��ȡֵ��Χ.
,��ʵ��a��ȡֵ��Χ.