题目内容
已知直线l经过点P(3,1),且被两平行直线l1:x+y+1=0和l2:x+y+6=0截得的线段之长为5,求直线l的方程.
x=3或y=1
(解法1)若直线l的斜率不存在,则直线l的方程为x=3,此时与l1、l2的交点分别为A′(3,-4)和B′(3,-9),截得的线段AB的长 =5,符合题意.
=5,符合题意.
若直线l的斜率存在,则设直线l的方程为y=k(x-3)+1.
解方程组 ,得A
,得A ,
,
解方程组 ,得B
,得B .
.
由 =5,得
=5,得 =52.
=52.
解之,得k=0,即所求的直线方程为y=1.综上可知,所求l的方程为x=3或y=1.
(解法2)由题意,直线l1、l2之间的距离为d= =
= ,且直线l被平行直线l1、l2所截得的线段AB的长为5(如图).
,且直线l被平行直线l1、l2所截得的线段AB的长为5(如图).

设直线l与直线l1的夹角为θ,则sinθ= ,故θ=45°.
,故θ=45°.
由直线l1:x+y+1=0的倾斜角为135°,知直线l的倾斜角为0°或90°.又直线l过点P(3,1),故直线l的方程为x=3或y=1.
(解法3)设直线l与l1、l2分别相交于A(x1,y1)、B(x2,y2),则x1+y1+1=0,x2+y2+6=0.
两式相减,得(x1-x2)+(y1-y2)=5.①
又(x1-x2)2+(y1-y2)2=25,②
联立①②,可得
由上可知,直线l的倾斜角分别为0°或90°.
故所求直线方程为x=3或y=1.
 =5,符合题意.
=5,符合题意.若直线l的斜率存在,则设直线l的方程为y=k(x-3)+1.
解方程组
 ,得A
,得A ,
,解方程组
 ,得B
,得B .
.由
 =5,得
=5,得 =52.
=52.解之,得k=0,即所求的直线方程为y=1.综上可知,所求l的方程为x=3或y=1.
(解法2)由题意,直线l1、l2之间的距离为d=
 =
= ,且直线l被平行直线l1、l2所截得的线段AB的长为5(如图).
,且直线l被平行直线l1、l2所截得的线段AB的长为5(如图).
设直线l与直线l1的夹角为θ,则sinθ=
 ,故θ=45°.
,故θ=45°.由直线l1:x+y+1=0的倾斜角为135°,知直线l的倾斜角为0°或90°.又直线l过点P(3,1),故直线l的方程为x=3或y=1.
(解法3)设直线l与l1、l2分别相交于A(x1,y1)、B(x2,y2),则x1+y1+1=0,x2+y2+6=0.
两式相减,得(x1-x2)+(y1-y2)=5.①
又(x1-x2)2+(y1-y2)2=25,②
联立①②,可得

由上可知,直线l的倾斜角分别为0°或90°.
故所求直线方程为x=3或y=1.

练习册系列答案
相关题目
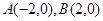 ,点
,点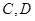 依次满足
依次满足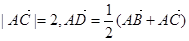 。
。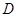 的轨迹;
的轨迹; 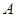 作直线
作直线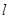 交以
交以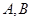 为焦点的椭圆于
为焦点的椭圆于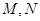 两点,线段
两点,线段 的中点到
的中点到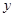 轴的距离为
轴的距离为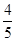 ,且直线
,且直线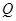 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点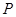 及以
及以 都相切,如存在,求出
都相切,如存在,求出 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦,
的弦,
 ;
; ,求点
,求点 中,点
中,点 的坐标分别为
的坐标分别为 则
则