题目内容
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
分析:(1)先根据二倍角公式以及配角公式化为基本三角函数,再代入求![]() 的值;(2)根据正弦函数性质确定单调性递增区间,再根据区间之间包含关系列不等式,解得实数
的值;(2)根据正弦函数性质确定单调性递增区间,再根据区间之间包含关系列不等式,解得实数![]() 的取值范围;(3)先根据正弦函数图像确定a的取值范围,再根据对称性得
的取值范围;(3)先根据正弦函数图像确定a的取值范围,再根据对称性得![]() ,最后代入求实数
,最后代入求实数![]() 的取值范围.
的取值范围.
详解:
(Ⅰ)∵![]()
![]()
![]()
∴![]()
(Ⅱ)由![]() ,
,![]()
得![]() ,
,![]()
∴![]() 在区间
在区间![]() 上是增函数
上是增函数
∴当![]() 时,
时,![]() 在区间
在区间![]() 上是增函数
上是增函数
若函数![]() 在区间
在区间![]() 上是单调递增函数,则
上是单调递增函数,则![]()
∴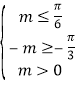 ,解得
,解得![]()
(Ⅲ)方程![]() 在区间
在区间![]() 内有两实数根
内有两实数根![]() 等价于直线
等价于直线![]() 与曲线
与曲线![]()
![]() 有两个交点.
有两个交点.
∵当![]() 时,由(Ⅱ)知
时,由(Ⅱ)知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且
上是减函数,且![]() ,
,![]() ,
,![]() ,
,
∴![]()
即实数![]() 的取值范围是
的取值范围是![]()
∵函数![]() 的图像关于
的图像关于![]() 对称
对称
∴![]() ,∴
,∴![]()
∴实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目


