题目内容
(本小题满分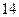 分)
分)
(Ⅰ)若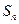 是公差不为零的等差数列
是公差不为零的等差数列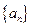 的前n项和,且
的前n项和,且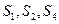 成等比数列,求数列
成等比数列,求数列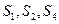 的公比;
的公比;
(II)设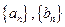 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,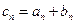 ,证明数列
,证明数列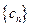 不是等比数列。
不是等比数列。
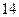 分)
分)(Ⅰ)若
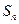 是公差不为零的等差数列
是公差不为零的等差数列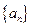 的前n项和,且
的前n项和,且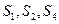 成等比数列,求数列
成等比数列,求数列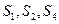 的公比;
的公比; (II)设
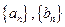 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,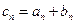 ,证明数列
,证明数列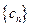 不是等比数列。
不是等比数列。(Ⅰ)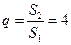
(II)证明略
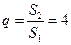
(II)证明略
解:(Ⅰ)设数列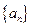 的公差为d,由题意,得
的公差为d,由题意,得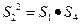

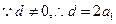
故公比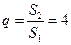 ……………7分
……………7分
(II)设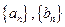 的公比分别是p、q(p≠q),
的公比分别是p、q(p≠q),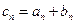
为证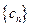 不是等比数列只需证
不是等比数列只需证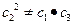 。 ………10分
。 ………10分
事实上,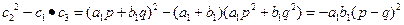 ,
,
由于p≠q,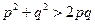 ,又
,又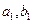 不为零,
不为零,
因此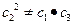 ,故
,故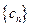 不是等比数列。……………………14分
不是等比数列。……………………14分
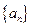 的公差为d,由题意,得
的公差为d,由题意,得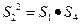

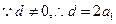
故公比
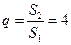 ……………7分
……………7分 (II)设
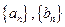 的公比分别是p、q(p≠q),
的公比分别是p、q(p≠q),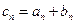
为证
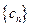 不是等比数列只需证
不是等比数列只需证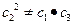 。 ………10分
。 ………10分事实上,
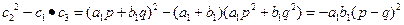 ,
,由于p≠q,
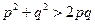 ,又
,又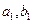 不为零,
不为零,因此
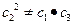 ,故
,故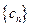 不是等比数列。……………………14分
不是等比数列。……………………14分
练习册系列答案
相关题目
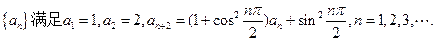
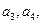 并求数列
并求数列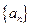 的通项公式;
的通项公式;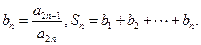 ,求
,求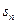 。
。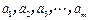 (
(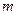 为正整数)满足条件
为正整数)满足条件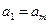 ,
,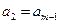 ,…,
,…,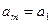 ,即
,即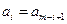 (
(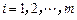 ),我们称其为“对称数列”.
),我们称其为“对称数列”. 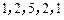 与数列
与数列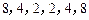 都是“对称数列”.
都是“对称数列”. 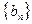 是7项的“对称数列”,其中
是7项的“对称数列”,其中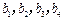 是等差数列,且
是等差数列,且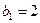 ,
,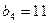 .依次写出
.依次写出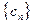 是
是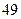 项的“对称数列”,其中
项的“对称数列”,其中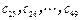 是首项为
是首项为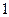 ,公比为
,公比为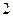 的等比数列,求
的等比数列,求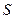 ;
;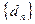 是
是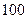 项的“对称数列”,其中
项的“对称数列”,其中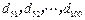 是首项为
是首项为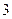 的等差数列.求
的等差数列.求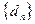 前
前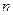 项的和
项的和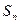
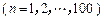 .
. 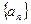 的前
的前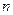 项和为
项和为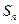 ,且
,且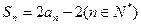 ,数列
,数列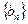 中,
中,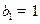 ,
,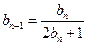 .(
.(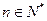 )
)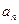 和
和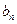
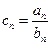 ,求数列
,求数列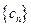 的前n项和
的前n项和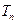 .
.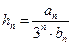 ,若对于一切
,若对于一切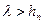 恒成立,求
恒成立,求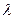 的取值范围
的取值范围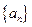 满足
满足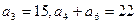 ,
,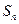 为
为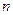 项和.
项和.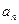 及当
及当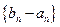 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列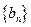 的通项公式及其前
的通项公式及其前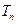 .
.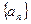 满足:
满足: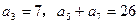 ,
,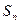 ,
,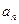 及
及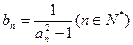 ,求数列
,求数列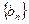 的前n项和
的前n项和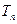 .
.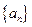 是公比为
是公比为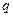 的等比数列,且
的等比数列,且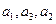 成等差数列,则公比
成等差数列,则公比



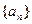 中,
中, 则
则 =" " ( )
=" " ( )