题目内容
设 A、B、C是直线l上的三点,向量
,
,
满足关系:
+(y-
sinxcosx)
-(
+sin2x)
=
.
(Ⅰ)化简函数y=f(x)的表达式;
(Ⅱ)若函数g(x)=f(
x+
),x∈[0,
]的图象与直线y=b的交点的横坐标成等差数列,试求实数b的值;
(Ⅲ)令函数h(x)=
(sinx+cosx)+sin2x-a,若对任意的x1,x2∈[0,
],不等式h(x1)≤f(x2)恒成立,求实数a的取值范围.
| OA |
| OB |
| OC |
| OA |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| 0 |
(Ⅰ)化简函数y=f(x)的表达式;
(Ⅱ)若函数g(x)=f(
| 1 |
| 2 |
| π |
| 3 |
| 7π |
| 12 |
(Ⅲ)令函数h(x)=
| 2 |
| π |
| 2 |
(Ⅰ)由已知可得
=(-y+
sinxcosx)
+(
+sin2x)
∵A、B、C三点共线,∴-y+
sinxcosx+
+sin2x=1----------------------------------------,(2分)
则y=
sinxcosx+sin2x-
=
sin2x-
cos2x=sin(2x-
)
∴f(x)=sin(2x-
)--------------------------------(4分)
(Ⅱ)可得函数g(x)=f(
x+
)=sin[2(
x+
)-
]=sin(x+
)=cosx,x∈[0,
]-----(5分)
设函数g(x)的图象与直线y=b的交点的横坐标分别为x1,x2,x3,且0≤x1<x2<x3≤
,
由已知,有x1+x3=2x2,另一方面,结合图象的对称性有
=π,
=2π--------------------(7分)
∴x1=2π-x2,x3=4π-x2,代入x1+x3=2x2,解得x2=
------------(8分)
再代入g(x)=cosx,得g(x2)=cos
=0,所以b=0------------------(9分)
(Ⅲ)不等式h(x1)≤f(x2)恒成立,只需要h(x)max≤f(x)min即可------------(10分)
令t=sinx+cosx=
sin(x+
),则t2=1+2sinxcosx=1+sin2x,∴sin2x=t2-1
又t=sinx+cosx=
sin(x+
),x∈[0,
],则t∈[1,
]
函数h(x)转化为y=
t+t2-1-a=(t+
)2-a-
,t∈[1,
],
当t=
时,函数取得最大值h(x)max=3-a-----------------------------------(12分)
又f(x)=sin(2x-
)在x∈[0,
]上的最小值为f(x)min=-
------------------(13分)
由h(x)max≤f(x)min得3-a≤-
即a≥
,
故实数a的取值范围是[
,+∞)--------14分
| OA |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
∵A、B、C三点共线,∴-y+
| 3 |
| 1 |
| 2 |
则y=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴f(x)=sin(2x-
| π |
| 6 |
(Ⅱ)可得函数g(x)=f(
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 7π |
| 2 |
设函数g(x)的图象与直线y=b的交点的横坐标分别为x1,x2,x3,且0≤x1<x2<x3≤
| 7π |
| 2 |
由已知,有x1+x3=2x2,另一方面,结合图象的对称性有
| x1+x2 |
| 2 |
| x2+x3 |
| 2 |
∴x1=2π-x2,x3=4π-x2,代入x1+x3=2x2,解得x2=
| 3π |
| 2 |
再代入g(x)=cosx,得g(x2)=cos
| 3π |
| 2 |
(Ⅲ)不等式h(x1)≤f(x2)恒成立,只需要h(x)max≤f(x)min即可------------(10分)
令t=sinx+cosx=
| 2 |
| π |
| 4 |
又t=sinx+cosx=
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2 |
函数h(x)转化为y=
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
当t=
| 2 |
又f(x)=sin(2x-
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
由h(x)max≤f(x)min得3-a≤-
| 1 |
| 2 |
| 7 |
| 2 |
故实数a的取值范围是[
| 7 |
| 2 |

练习册系列答案
相关题目
 满足关系:
满足关系: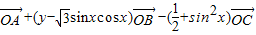 =
=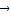 .
.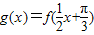 ,
,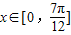 的图象与直线y=b的交点的横坐标成等差数列,试求实数b的值;
的图象与直线y=b的交点的横坐标成等差数列,试求实数b的值;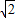 (sinx+cosx)+sin2x-a,若对任意的
(sinx+cosx)+sin2x-a,若对任意的 ,不等式h(x1)≤f(x2)恒成立,求实数a的取值范围.
,不等式h(x1)≤f(x2)恒成立,求实数a的取值范围.