题目内容
如图,圆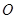 是
是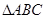 的外接圆,过点C的切线交
的外接圆,过点C的切线交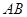 的延长线于点
的延长线于点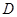 ,
,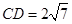 ,
,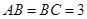 .则
.则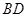 的长为 ;
的长为 ;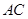 的长为 .
的长为 .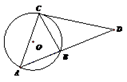
 是
是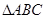 的外接圆,过点C的切线交
的外接圆,过点C的切线交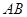 的延长线于点
的延长线于点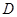 ,
,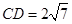 ,
,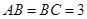 .则
.则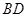 的长为 ;
的长为 ;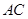 的长为 .
的长为 .
4,

根据弦切角定理发现∠BCD=∠A,结合公共角发现△BCD∽△CAD;然后根据三条对应边的比相等进行求解.
解:∵CD是圆的切线,
∴∠BCD=∠A;
又∠D=∠D,
∴△BCD∽△CAD,
∴ ,
,
即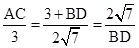 ,
,
则BD=4或-7(负值舍去).
所以AC= .
.
考查的是切线的性质、相似三角形的判定和性质.
解:∵CD是圆的切线,
∴∠BCD=∠A;
又∠D=∠D,
∴△BCD∽△CAD,
∴
 ,
,即
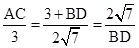 ,
,则BD=4或-7(负值舍去).
所以AC=
 .
.考查的是切线的性质、相似三角形的判定和性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
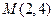 向圆
向圆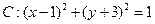 所引的切线方程;
所引的切线方程;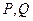 ,求直线
,求直线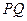 的方程。
的方程。 与圆
与圆 交于
交于 两点,且
两点,且 对称,求不等式组
对称,求不等式组 表示的平面区域的面积
表示的平面区域的面积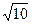 ,圆心在直线
,圆心在直线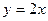 上,圆被直线
上,圆被直线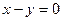 截得的弦长为
截得的弦长为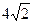 ,求圆的方程.
,求圆的方程.


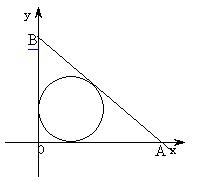
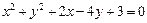
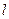 与圆C相切,且直线
与圆C相切,且直线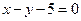 距离的最大值与最小值
距离的最大值与最小值 对称,则ab的取值范围是 ( )
对称,则ab的取值范围是 ( )
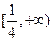


 ,则
,则 的大小为 .
的大小为 .