题目内容
设命题q:在x∈(0,2]内,不等式x2-
+3≥0恒成立;命题q:方程
+
=1表示双曲线.
(1)若命题q为真命题,求实数m的取值范围;
(2)若命题:“p∨q”为真命题,且“p∧q”为假命题,求实数m的取值范围.
| x |
| m |
| x2 |
| m-3 |
| y2 |
| 5-m |
(1)若命题q为真命题,求实数m的取值范围;
(2)若命题:“p∨q”为真命题,且“p∧q”为假命题,求实数m的取值范围.
分析:(1)利用求函数f(x)=x2-
+3,在x∈(0,2]时的最小值的方法,分类讨论解答即可;
(2)先求出命题q为真命题时,m的取值范围,再根据复合命题真值表求解即可.
| x |
| m |
(2)先求出命题q为真命题时,m的取值范围,再根据复合命题真值表求解即可.
解答:解:(1)设函数f(x)=x2-
+3,在x∈(0,2]时的最小值为g(m),
①当对称轴x=
≤0时,即m<0时,∵f(0)=3>0,∴不等式x2-
+3≥0恒成立;
②当x=
≥2时,即0<m≤
时,g(m)=f(2)=4-
+3=7-
≥0?m≥
或m<0,
∴此时m∈∅;
③当0<
<2,即m>
时,g(m)=3-
≥0?m≥
.
综上:命题q为真命题,实数m的取值范围是m<0或m≥
.
(2)命题q为真命题的m的取值范围是(m-3)(5-m)<0?m>5或m<3,
∵“p∨q”为真命题,且“p∧q”为假命题,根据复合命题真值表得:命题P、命题q一真一假,
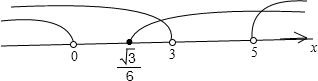
故m的取值范围是:3≤m≤5或0≤m<
.
| x |
| m |
①当对称轴x=
| 1 |
| 2m |
| x |
| m |
②当x=
| 1 |
| 2m |
| 1 |
| 4 |
| 2 |
| m |
| 2 |
| m |
| 2 |
| 7 |
∴此时m∈∅;
③当0<
| 1 |
| 2m |
| 1 |
| 4 |
| 1 |
| 4m2 |
| ||
| 6 |
综上:命题q为真命题,实数m的取值范围是m<0或m≥
| ||
| 6 |
(2)命题q为真命题的m的取值范围是(m-3)(5-m)<0?m>5或m<3,
∵“p∨q”为真命题,且“p∧q”为假命题,根据复合命题真值表得:命题P、命题q一真一假,

故m的取值范围是:3≤m≤5或0≤m<
| ||
| 6 |
点评:本题借助考查复合命题的真假判定,考查不等式的恒成立问题,不等式的恒成立问题可结合函数,利用数形结合思想来分析解答.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目