题目内容
(本小题满分12分).设p:实数x满足 ,其中
,其中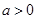 ,命题
,命题 实数
实数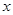 满足
满足 .
.
(I)若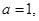 且
且 为真,求实数
为真,求实数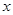 的取值范围;
的取值范围;
(II)若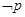 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
(1)2<x<3; (2) 1<a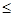 2.
2.
解析试题分析:(1)当a=1时,p真:1<x<3,q真:2<x≤4,由p∧q为真,能求出x的取值范围.
(2)若¬p是¬q的充分不必要条件,则q是p的充分不必要条件,由a>0,知p:a<x<3a,q:2<x≤4,由此能求出a的取值范围。
解:(1)P:(x-1)(x—3)<0, 则1<x<3
q :  则
则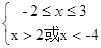 所以2<x
所以2<x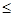 3
3
则  为真,实数
为真,实数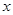 的取值范围 2<x<3
的取值范围 2<x<3
(2) 若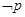 是
是
 的充分不必要条件, 则q是p的充分不必要条件
的充分不必要条件, 则q是p的充分不必要条件
{x|2<x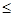 3}
3} {x|a<x<3a}
{x|a<x<3a}
所以a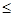 2且3a>3 所以实数a的取值范围1<a
2且3a>3 所以实数a的取值范围1<a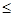 2.
2.
考点:本试题主要考查了复合命题的应用和必要条件、充分条件、充要条件的应用,是基础题.解题时要认真审题,仔细解答.
点评:解决该试题的关键是准确表示命题P,Q的集合,进而利用复合命题的真值问题,结合交集和子集的关系得到结论。

练习册系列答案
相关题目
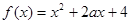 有零点;
有零点;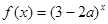 是增函数,
是增函数,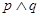 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.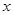 都有
都有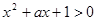 恒成立;命题q :关于
恒成立;命题q :关于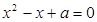 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数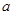 的取值范围。
的取值范围。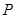 :函数
:函数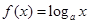 在
在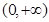 上是增函数;命题
上是增函数;命题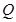 :
: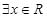 ,使得
,使得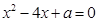 .
.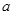 的取值范围;
的取值范围;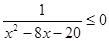 ,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围. 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.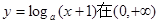 内单调递减;命题Q:曲线
内单调递减;命题Q:曲线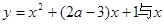 轴交于不同的两点.
轴交于不同的两点.  :关于
:关于 的不等式
的不等式 对于一切
对于一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围; 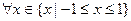 ,都有不等式
,都有不等式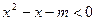 成立”是真命题。
成立”是真命题。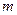 的取值集合
的取值集合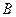 ;
; 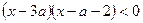 的解集为
的解集为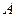 ,若
,若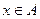 是
是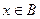 的充分不必要条件,求实数
的充分不必要条件,求实数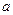 的取值范围.
的取值范围.