题目内容
(本题12分)
设命题P:函数 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
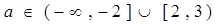 。
。
解析试题分析:p为真命题?f'(x)=3x2-a≤0在[-1,1]上恒成立?a≥3x2在[-1,1]上恒成立?a≥3
q为真命题?△=a2-4≥0恒成立?a≤-2或a≥2
由题意P和q有且只有一个是真命题p真q假?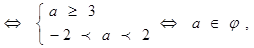
p假q真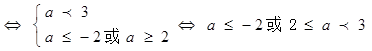 ?a≤-2或2≤a<3
?a≤-2或2≤a<3
综上所述:a∈(-∞,-2]∪[2,3)
考点:本试题主要考查了命题的真假判断和应用,解题时要注意合理地进行等价转化。
点评:解决该试题的关键由p为真命题,能够推导出a≥3.再由q为真命题,能够推导出a≤-2或a≥2.由题意P和q有且只有一个是真命题,所以p真q假? a≥3,-2< a <2,p假q真?a≤-2或2≤a<3.由此能够得到a的取值范围

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
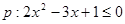 和命题
和命题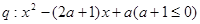 ,若
,若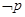 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.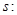 方程
方程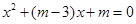 的一根在
的一根在 内,另一根在
内,另一根在 内.
内.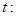 函数
函数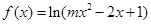 的定义域为全体实数.
的定义域为全体实数. 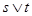 为真命题,求实数
为真命题,求实数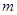 的取值范围.
的取值范围.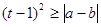 ,其中
,其中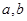 满足条件:五个数
满足条件:五个数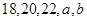 的平均数是20,标准差是
的平均数是20,标准差是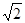 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆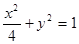 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。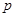 :方程
:方程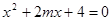 有实数根;命题
有实数根;命题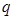 :方程
:方程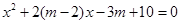 有实数根.已知
有实数根.已知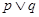 为真,
为真,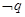 为真,求实数
为真,求实数 的取值范围.
的取值范围. ,其中
,其中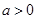 ,命题
,命题 实数
实数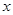 满足
满足 .
. 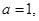 且
且 为真,求实数
为真,求实数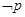 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. :
: 是减函数,命题
是减函数,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ,如果“
,如果“ 的取值范围.
的取值范围.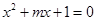 有两个不等的负根;
有两个不等的负根;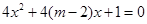 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,
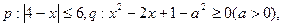 若非
若非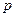 是
是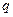 的充分不必要条件,求
的充分不必要条件,求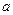 的取值范围。
的取值范围。