题目内容

已知定义域为的函数同时满足以下三个条件：

[1] 对任意的，总有；

[2] ；

[3] 若，，且，则有成立，

并且称为“友谊函数”，请解答下列各题：

(1)若已知为“友谊函数”，求的值；

(2)函数在区间上是否为“友谊函数”？并给出理由.

(3)已知为“友谊函数”，假定存在，使得且，

求证：.

解析：（1）取得，又由，得

（2）显然在上满足[1] ；[2] .若，，且，则有

故满足条件[1]、[2]、[3]，所以为友谊函数.

(3)由 [3]知任给其中，且有，不妨设

则必有：所以：

所以：.依题意必有,

下面用反证法证明：假设，则有或

(1) 若，则，这与矛盾；

(2) 若，则，这与矛盾；

故由上述（1）、（2）证明知假设不成立，则必有，证毕.

练习册系列答案

单元测试卷湖南教育出版社系列答案

单元达标卷系列答案

单元过关目标检测卷系列答案

天舟文化单元练测卷系列答案

单元巧练章节复习手册系列答案

学习指导与评价系列答案

单元综合练习与检测AB卷系列答案

导思学案系列答案

导学精练中考总复习系列答案

导学练小学毕业总复习系列答案

相关题目

定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=Inx，g（x）=1-

（I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
（Ⅱ）设P（x₁，f（x₁）），Q（x₂，f（x₂））是函数 f（x）图象上任意两点，且0＜x₁＜x₂，若存在实数x₃＞0，使得f′（x₃）=

．请结合（I）中的结论证明x₁＜x₃＜x₂．

若函数f（x）的定义域与值域都为同一区间D，则称函数f（x）为区间D上的“同势”函数．已知函数f（x）=x²-2x+1是区间D上的“同势”函数，则此区间可以是

]或[0，1]或[

]或[0，1]或[

．（只要写出一个你认为正确的区间即可）

定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足f（x）≤g（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=lnx，g（x）=1-

．
（1）试探求f（x）与g（x）是否存在“左同旁切线”，若存在，请求出左同旁切线方程；若不存在，请说明理由．
（2）设P（x₁，f（x₁）），Q（x₂，f（x₂））是函数f（x）图象上任意两点，0＜x₁＜x₂，且存在实数x₃＞0，使得f（x₃）=

，证明：x₁＜x₃＜x₂．

定义：已知函数f（x）与g（x），若存在一条直线y=kx +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx +b为曲线f（x）与g（x）的“左同旁切线”．已知

（I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；

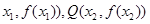（Ⅱ）设P（是函数 f（x）图象上任意两点，且0<x₁<x₂，若存在实数x₃>0，使得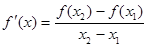．请结合（I）中的结论证明：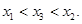

定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=Inx，g（x）=1- $数学公式$
（I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
（Ⅱ）设P（x₁，f（x₁）），Q（x₂，f（x₂））是函数 f（x）图象上任意两点，且0＜x₁＜x₂，若存在实数x₃＞0，使得f′（x₃）= $数学公式$ ．请结合（I）中的结论证明x₁＜x₃＜x₂．