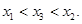题目内容
定义:已知函数f(x)与g(x),若存在一条直线y=kx+b,使得对公共定义域内的任意实数均满足f(x)≤g(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx+b为曲线f(x)与g(x)的“左同旁切线”.已知f(x)=lnx,g(x)=1-
.
(1)试探求f(x)与g(x)是否存在“左同旁切线”,若存在,请求出左同旁切线方程;若不存在,请说明理由.
(2)设P(x1,f(x1)),Q(x2,f(x2))是函数f(x)图象上任意两点,0<x1<x2,且存在实数x3>0,使得f(x3)=
,证明:x1<x3<x2.
| 1 |
| x |
(1)试探求f(x)与g(x)是否存在“左同旁切线”,若存在,请求出左同旁切线方程;若不存在,请说明理由.
(2)设P(x1,f(x1)),Q(x2,f(x2))是函数f(x)图象上任意两点,0<x1<x2,且存在实数x3>0,使得f(x3)=
| f(x2)-f(x1) |
| x2-x1 |
分析:(1)由题意知f(x)与g(x)有公共点,确定在公共点处的切线方程为y=x-1,再证y=x-1就是左同旁切线方程,即证1-
≤lnx≤x-1(x>0);
(2)利用反证法进行证明,令x3≤x1,则x3=
≤x1,从而可得x2-x1≤x1ln
<x1(
-1)=x2-x1,由此得证.
| 1 |
| x |
(2)利用反证法进行证明,令x3≤x1,则x3=
| x2-x1 | ||
ln
|
| x2 |
| x1 |
| x2 |
| x1 |
解答:解:(1)由题意知f(x)与g(x)有公共点,令其为(x0,y0),则f(x0)=f(x0),f'(x0)=g'(x0),即
,解得x0=1,y0=1.
所以在公共点处的切线方程为y=x-1.
下证y=x-1就是左同旁切线方程,即证1-
≤lnx≤x-1(x>0).
先构造函数h(x)=lnx-x+1(x>0),则h'(x)=
-1=
,
令h'(x)>0可得0<x<1,h'(x)<0可得x<0或x>1,
∴函数在x=1处h(x)取得最大值h(1)=0,所以lnx-x+1≤0,即lnx≤x-1(x>0).(4分)
再构造函数φ(x)=lnx-1+
(x>0),则φ′(x)=
,
令φ'(x)>0可得x>1,φ'(x)<0可得x<1,
∴在x=1处φ(x)取得最小值φ(1)=0,所以lnx-1+
≥0,即lnx≥1-
(x>0).
故对任意x∈(0,+∞),恒有1-
≤lnx≤x-1(x>0)成立,即y=x-1就是左同旁切线方程.(6分)
(2)因为f′(x)=
,所以f′(x3)=
=
=
,所以x3=
.
令x3≤x1,则x3=
≤x1,
∴x2-x1≤x1ln
<x1(
-1)=x2-x1,
显然自相矛盾,故x1<x3;同理可证x3<x2.
故x1<x3<x2.(12分)
|
所以在公共点处的切线方程为y=x-1.
下证y=x-1就是左同旁切线方程,即证1-
| 1 |
| x |
先构造函数h(x)=lnx-x+1(x>0),则h'(x)=
| 1 |
| x |
| 1-x |
| x |
令h'(x)>0可得0<x<1,h'(x)<0可得x<0或x>1,
∴函数在x=1处h(x)取得最大值h(1)=0,所以lnx-x+1≤0,即lnx≤x-1(x>0).(4分)
再构造函数φ(x)=lnx-1+
| 1 |
| x |
| x-1 |
| x2 |
令φ'(x)>0可得x>1,φ'(x)<0可得x<1,
∴在x=1处φ(x)取得最小值φ(1)=0,所以lnx-1+
| 1 |
| x |
| 1 |
| x |
故对任意x∈(0,+∞),恒有1-
| 1 |
| x |
(2)因为f′(x)=
| 1 |
| x |
| 1 |
| x3 |
| lnx2-lnx1 |
| x2-x1 |
ln
| ||
| x2-x1 |
| x2-x1 | ||
ln
|
令x3≤x1,则x3=
| x2-x1 | ||
ln
|
∴x2-x1≤x1ln
| x2 |
| x1 |
| x2 |
| x1 |
显然自相矛盾,故x1<x3;同理可证x3<x2.
故x1<x3<x2.(12分)
点评:本题考查导数知识的运用,考查新定义,考查函数的最值,正确理解新定义是关键.

练习册系列答案
相关题目
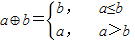 已知函数f(x)=x2⊕x,求f(2)= .
已知函数f(x)=x2⊕x,求f(2)= .
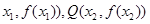 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得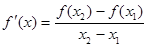 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: