题目内容
定义:已知函数f(x)与g(x),若存在一条直线y=kx +b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx +b为曲线f(x)与g(x)的“左同旁切线”.已知
(I)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(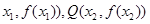 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得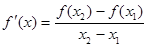 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: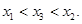
【答案】
(Ⅰ)见解析 (Ⅱ)见解析
【解析】本试题主要是考查了导数在研究函数中的运用,研究函数的单调性和最值,以及函数与不等式的综合运用。
(Ⅰ)要证明结论即证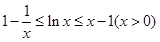 .
.
构造函数令 ,则
,则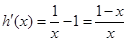 ,分析最值得到结论。
,分析最值得到结论。
再令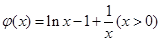 分析最值得到结论
分析最值得到结论
综上可知故对任意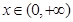 ,恒有
,恒有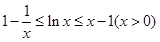 成立,即直线
成立,即直线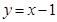 是
是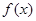 与
与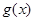 的“左同旁切线”
的“左同旁切线”
(Ⅱ)因为根据已知函数,得到导函数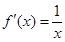 ,所以
,所以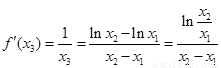 ,所以
,所以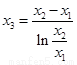 .采用作差法,利用(Ⅰ)的结论因为
.采用作差法,利用(Ⅰ)的结论因为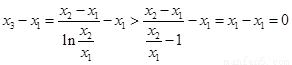 得到。
得到。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
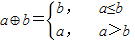 已知函数f(x)=x2⊕x,求f(2)= .
已知函数f(x)=x2⊕x,求f(2)= .