��Ŀ����
���壺��֪����f��x����g��x����������һ��ֱ��y=kx+b��ʹ�öԹ����������ڵ�����ʵ��������g��x����f��x����kx+b����������еȺ��ڹ����㴦���������ֱ��y=kx+bΪ����f��x����g��x���ġ���ͬ�����ߡ�����֪f��x��=Inx��g��x��=1-
��I��֤����ֱ��y=x-l��f��x����g��x���ġ���ͬ�����ߡ���
������P��x1��f��x1������Q��x2��f��x2�����Ǻ��� f��x��ͼ�����������㣬��0��x1��x2��������ʵ��x3��0��ʹ��f�䣨x3��=
�����ϣ�I���еĽ���֤��x1��x3��x2��
| 1 |
| x |
��I��֤����ֱ��y=x-l��f��x����g��x���ġ���ͬ�����ߡ���
������P��x1��f��x1������Q��x2��f��x2�����Ǻ��� f��x��ͼ�����������㣬��0��x1��x2��������ʵ��x3��0��ʹ��f�䣨x3��=
| f(x2)-f(x1) |
| x2-x1 |
��������I��������֪f��x����g��x���ڹ����㴦�����߷���Ϊy=x-1����֤y=x-1������ͬ�����߷��̣���֤1-
��lnx��x-1��x��0��������ͨ�����캯�����õ����о�����ֵ����֤�������
��II�����÷�֤������֤������x3��x1����x3=
��x1���Ӷ��ɵ�x2-x1��x1ln
��x1��
-1��=x2-x1���ɴ˵�֤��
| 1 |
| x |
��II�����÷�֤������֤������x3��x1����x3=
| x2-x1 | ||
ln
|
| x2 |
| x1 |
| x2 |
| x1 |
����⣺��I����֤y=x-1������ͬ�����߷��̣���֤1-
��lnx��x-1��x��0����
�ȹ��캯��h��x��=lnx-x+1��x��0������h'��x��=
-1=
��
��h'��x����0�ɵ�0��x��1��h'��x����0�ɵ�x��0��x��1��
�ຯ����x=1��h��x��ȡ�����ֵh��1��=0������lnx-x+1��0����lnx��x-1��x��0������4�֣�
�ٹ��캯���գ�x��=lnx-1+
��x��0������ա䣨x��=
��
���'��x����0�ɵ�x��1����'��x����0�ɵ�x��1��
����x=1���գ�x��ȡ����Сֵ�գ�1��=0������lnx-1+
��0����lnx��1-
��x��0����
�ʶ�����x�ʣ�0��+�ޣ�������1-
��lnx��x-1��x��0��������
��y=x-1������ͬ�����߷��̣���6�֣�
��II����Ϊf�䣨x��=
������f�䣨x3��=
=
=
������x3=
��
��x3��x1����x3=
��x1��
��x2-x1��x1ln
��x1��
-1��=x2-x1��
��Ȼ����ì�ܣ���x1��x3��ͬ����֤x3��x2��
��x1��x3��x2����12�֣�
| 1 |
| x |
�ȹ��캯��h��x��=lnx-x+1��x��0������h'��x��=
| 1 |
| x |
| 1-x |
| x |
��h'��x����0�ɵ�0��x��1��h'��x����0�ɵ�x��0��x��1��
�ຯ����x=1��h��x��ȡ�����ֵh��1��=0������lnx-x+1��0����lnx��x-1��x��0������4�֣�
�ٹ��캯���գ�x��=lnx-1+
| 1 |
| x |
| x-1 |
| x2 |
���'��x����0�ɵ�x��1����'��x����0�ɵ�x��1��
����x=1���գ�x��ȡ����Сֵ�գ�1��=0������lnx-1+
| 1 |
| x |
| 1 |
| x |
�ʶ�����x�ʣ�0��+�ޣ�������1-
| 1 |
| x |
��y=x-1������ͬ�����߷��̣���6�֣�
��II����Ϊf�䣨x��=
| 1 |
| x |
| 1 |
| x3 |
| lnx2-lnx1 |
| x2-x1 |
ln
| ||
| x2-x1 |
| x2-x1 | ||
ln
|
��x3��x1����x3=
| x2-x1 | ||
ln
|
��x2-x1��x1ln
| x2 |
| x1 |
| x2 |
| x1 |
��Ȼ����ì�ܣ���x1��x3��ͬ����֤x3��x2��
��x1��x3��x2����12�֣�
���������⿼�鵼��֪ʶ�����ã������¶��壬���麯������ֵ����ȷ�����¶����ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
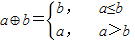 ��֪����f��x��=x2��x����f��2��= ��
��֪����f��x��=x2��x����f��2��= ��
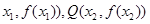 �Ǻ��� f��x��ͼ�����������㣬��0<x1<x2��������ʵ��x3>0��ʹ��
�Ǻ��� f��x��ͼ�����������㣬��0<x1<x2��������ʵ��x3>0��ʹ��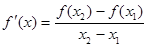 �����ϣ�I���еĽ���֤����
�����ϣ�I���еĽ���֤����