题目内容
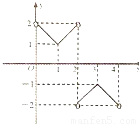
已知函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,给出下列命题:①是奇函数;
②|f(x)|的值域是[1,2);
③关于x的方程f2(x)-(a+2)f(x)+2a=0(a∈R)必有实根;
④关于x的不等式f(x)+kx+b≥0(k、b∈R且k≠0)的解集非空.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
【答案】分析:由函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,知函数y=f(x)是奇函数,|f(x)|的值域是[1,2);关于x的方程f2(x)-(a+2)f(x)+2a=0(a∈R)等价于:[f(x)-2][f(x)-a]=0,当|a|≥2时,无解;关于x的不等式f(x)+kx+b≥0(k、b∈R且k≠0)的解集非空.
解答:解:∵函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,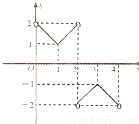
∴函数y=f(x)是奇函数,|f(x)|的值域是[1,2),
故①和②都正确;
③关于x的方程f2(x)-(a+2)f(x)+2a=0(a∈R)等价于:
[f(x)-2][f(x)-a]=0,即f(x)=2,或f(x)=a,
∴当|a|≥2时,无解,故③不正确;
④关于x的不等式f(x)+kx+b≥0(k、b∈R且k≠0)的解集非空,正确.
故选B.
点评:本题考查命题的真假判断及其应用,是基础题.解题时要认真审题,仔细解答,注意数形结合思想的合理运用.
解答:解:∵函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,

∴函数y=f(x)是奇函数,|f(x)|的值域是[1,2),
故①和②都正确;
③关于x的方程f2(x)-(a+2)f(x)+2a=0(a∈R)等价于:
[f(x)-2][f(x)-a]=0,即f(x)=2,或f(x)=a,
∴当|a|≥2时,无解,故③不正确;
④关于x的不等式f(x)+kx+b≥0(k、b∈R且k≠0)的解集非空,正确.
故选B.
点评:本题考查命题的真假判断及其应用,是基础题.解题时要认真审题,仔细解答,注意数形结合思想的合理运用.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足