题目内容
4.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,若对于满足约束条件的所有x,y,总有不等式y≤k(x+3)成立,则实数k的最小值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 0 |
分析 由题意作平面区域,从而化不等式为k≥$\frac{y}{x+3}$,而$\frac{y}{x+3}$的几何意义是点A(-3,0)与点(x,y)的连线的斜率,从而结合图象解得.
解答 解:由题意作平面区域如下,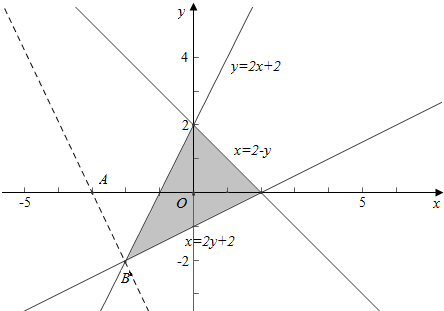 ,
,
结合图象可知,x≥-2,故x+3≥1,
故y≤k(x+3)可化为k≥$\frac{y}{x+3}$,
$\frac{y}{x+3}$的几何意义是点A(-3,0)与点(x,y)的连线的斜率,
故当过点B(-2,-2)时,$\frac{y}{x+3}$有最小值$\frac{-2}{-2+3}$=-2,
当过点(0,2)时,$\frac{y}{x+3}$有最大值$\frac{2-0}{0+3}$=$\frac{2}{3}$,
∵对于满足约束条件的所有x,y,总有不等式y≤k(x+3)成立,
∴实数k的最小值为$\frac{2}{3}$,
故选:B.
点评 本题考查了数形结合的思想应用及线性规划的应用,同时考查了恒成立问题.

练习册系列答案
相关题目
14.阅读如图所示程序框图,运行相应的程序,则输出的结果是( )
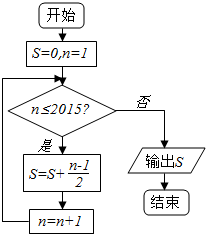

| A. | $\frac{2015×2016}{4}$ | B. | $\frac{2014×2015}{4}$ | C. | $\frac{2015×2016}{2}$ | D. | $\frac{2014×2015}{2}$ |
9.已知集合M={x|x>1},N={x|x2-2x≥0},则(∁RM)∩N=( )
| A. | (-∞,-2] | B. | (-∞,0] | C. | [0,1) | D. | [-2,0] |