Question

7．已知不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-m≤0}\\{y≥0}\end{array}\right.$表示平面区域Ω，其中x，y是变量，m∈R，若目标函数z=ax+6y（0＜a＜6）的最大值为19，最小值为-6，则平面区域Ω的面积为（　　）

• A． $\frac{25}{6}$
• B． $\frac{25}{3}$
• C． $\frac{50}{3}$
• D． 25

Answer 1

分析 作出不等式组对应的平面区域，利用目标函数的几何意义确定最优解，先求出a=3，然后求出m，即可得到结论．

解答 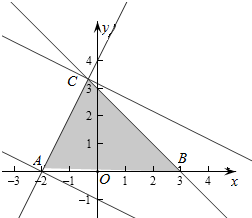解：作出不等式组对应的平面区域如图：
由z=ax+6y（0＜a＜6）得y=-$\frac{a}{6}$x+$\frac{z}{6}$，
则直线斜率-$\frac{a}{6}$∈（-1，0），
平移直线y=-$\frac{a}{6}$x+$\frac{z}{6}$，
由图象知当直线y=-$\frac{a}{6}$x+$\frac{z}{6}$经过点A时，直线的截距最小，此时z最小，为-6，
经过C点时，直线截距最大，此时z最大为19，
由$\left\{\begin{array}{l}{2x-y+4=0}\\{y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$，
即A（-2，0），
此时-2a+0=-6，
解得a=3，即目标函数z=3x+6y，
由$\left\{\begin{array}{l}{3x+6y=19}\\{2x-y+4=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{1}{3}}\\{y=\frac{10}{3}}\end{array}\right.$，即C（$-\frac{1}{3}$，$\frac{10}{3}$），
同时C（$-\frac{1}{3}$，$\frac{10}{3}$），也在直线x+y-m=0上，
∴$-\frac{1}{3}$+$\frac{10}{3}$-m=0，解得m=3，
即直线为x+y-3=0，
当y=0时，x=3，即B（3，0），
则三角形的面积S=$\frac{1}{2}$×（3+2）×$\frac{10}{3}$=$\frac{25}{3}$，
故选：B．

点评 本题主要考查线性规划的应用，利用数形结合是解决线性规划问题中的基本方法．考查学生的运算和推理能力．